学习笔记

Mamba

我们假设在时间步 tt 的输入为 xt∈RDx_t\in \R^{D}，序列长度为 LL。在 Mamba 中，我们将 xtx_t 的每一维看做一个独立变化的函数。我们用额外的 NN 维向量来作为隐状态 h∈RNh\in \R^N，用于近似这个函数。我们假设 xx 某一维随 tt 变化的函数为 u:R↦Ru: \R\mapsto \R

h′(t)=Ah(t)+Bu(t)y(t)=Ch(t)\begin{aligned} \mathbf h'(t) &= A \mathbf h(t) +B u(t) \\ y(t) &= C \mathbf h(t) \end{aligned}

其中 A=diag(α1,⋯ ,αH)∈RN×N,B,C∈RNA =\text{diag}(\alpha_1, \cdots, \alpha_H)\in \R^{N\times N}, B, C\in \R^{N}。

Zero-Order Hold 假设 ZOH 假设在两个离散的采样点之间，u(t)u(t) 保持不变：

u(t)=uk      ,if t∈(tk−1,tk]u(t) = u_k\ \ \ \ \ \ ,\text{if}\ t\in (t_{k-1}, t_k]

离散化 将两端乘上 e−Ate^{-At} 有

e−Ath′(t)=e−AtAh(t)+e−AtBu(t)e−Ath′(t)−e−AtAh(t)=e−AtBu(t)d(e−Ath(t))dt=e−AtBu(t)h(t)=eAt(C+∫e−AτBu(τ)dτ)\begin{aligned} e^{-At}\mathbf h'(t) &= e^{-At}A \mathbf h(t) + e^{-At}B u(t) \\ e^{-At}\mathbf h'(t) - e^{-At}A \mathbf h(t) &= e^{-At}B u(t) \\ \frac{\text d(e^{-At}\mathbf h(t) )}{\text{d}t} &= e^{-At}B u(t) \\ \mathbf h(t)&= e^{At}\left (C+ \int e^{-A\tau }Bu(\tau) \text d \tau \right ) \end{aligned}

分别取 t=tk−1,tkt = t_{k - 1}, t_{k}，那么有：

hk−1=eAtk−1(C+∫0tk−1e−AτBu(τ)dτ)hk=eAtk(C+∫0tke−AτBu(τ)dτ)=eA(tk−tk−1)⋅eAtk−1(C+∫0tk−1e−AτBu(τ)dτ)    +eAtk∫tk−1tke−AτBu(τ)dτ=eA(tk−tk−1)hk−1+eAtk∫tk−1tke−AτBu(τ)dτ\begin{aligned} h_{k-1}&= e^{At_{k-1}}\left (C+ \int_0^{t_{k-1}} e^{-A\tau }Bu(\tau) \text d \tau \right ) \\ h_{k}&= e^{At_{k}}\left (C+ \int_0^{t_{k}} e^{-A\tau }Bu(\tau) \text d \tau \right ) \\ &= e^{A(t_{k}-t_{k-1})} \cdot e^{At_{k-1}}\left (C+ \int_0^{t_{k-1}} e^{-A\tau }Bu(\tau) \text d \tau \right ) \\ & \ \ \ \ + e^{At_k }\int_{t_{k-1}}^{t_{k}} e^{-A\tau }Bu(\tau) \text d \tau \\ &= e^{A(t_k - t_{k-1})} h_{k-1} + e^{At_k}\int_{t_{k-1}}^{t_{k}} e^{-A\tau }Bu(\tau) \text d \tau \end{aligned}

令 Δk=tk−tk−1\Delta_k = t_{k} - t_{k - 1}，那么有

hk=eAΔhk−1+eAtk(∫tk−1tke−Aτdτ)Buk=eAΔhk−1+eAtkA−1(e−Atk−1−e−Atk)Buk=eAΔhk−1+A−1(eAΔ−I)Buk\begin{aligned} h_k &= e^{A\Delta }h_{k - 1} + e^{At_k}\left (\int_{t_{k-1}}^{t_k} e^{-A\tau }\text d\tau \right ) Bu_k \\ &= e^{A\Delta }h_{k - 1} + e^{At_k}A^{-1} \left (e^{-A t_{k-1} } - e^{-At_k} \right ) Bu_k \\ &= e^{A\Delta }h_{k - 1} + A^{-1}(e^{A\Delta } -I)Bu_k \end{aligned}

因此有

Aˉ=eΔA,Bˉ=(ΔA)−1(eΔA−I)ΔB\begin{aligned} \bar A = e^{\Delta A}, \bar B = (\Delta A)^{-1} (e^{\Delta A}- I)\Delta B \end{aligned}

Selective State Space Model

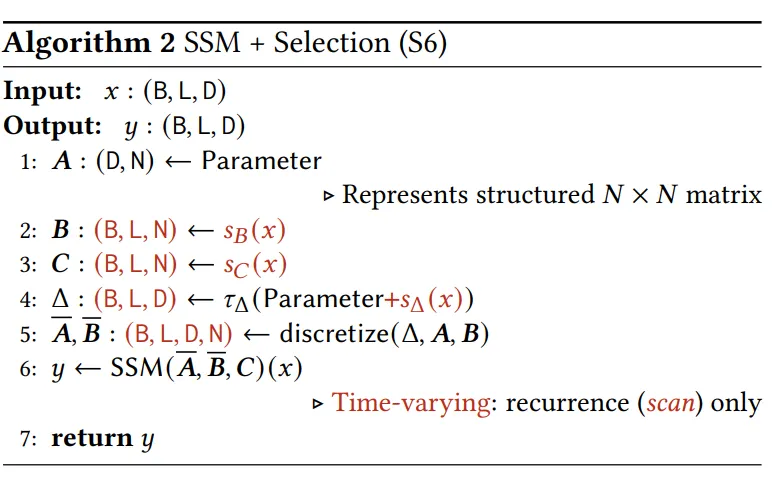
SSM + Selection

Mamba 不采用常数的 B, C 矩阵，而是将 B, C 改为输出 xtx_t 相关，通过一次投影计算。对于输入 xtx_t 每一维度，均使用一个独立的步长，由输入 xtx_t 投影并加上偏置得到。由于 BB 也是一个与 tt 有关的变量，上面的积分部分 ∫tk−1tke−AτBu(τ)dτ\int_{t_{k-1}}^{t_{k}} e^{-A\tau }Bu(\tau) \text d \tau 直接用右端的函数值近似为一个矩形，Mamba 实际采用的离散化方式是

ht≈eΔtAtht−1+ΔtBtxth_t \approx e^{\Delta_t A_t} h_{t-1}+\Delta _t B_t x_t

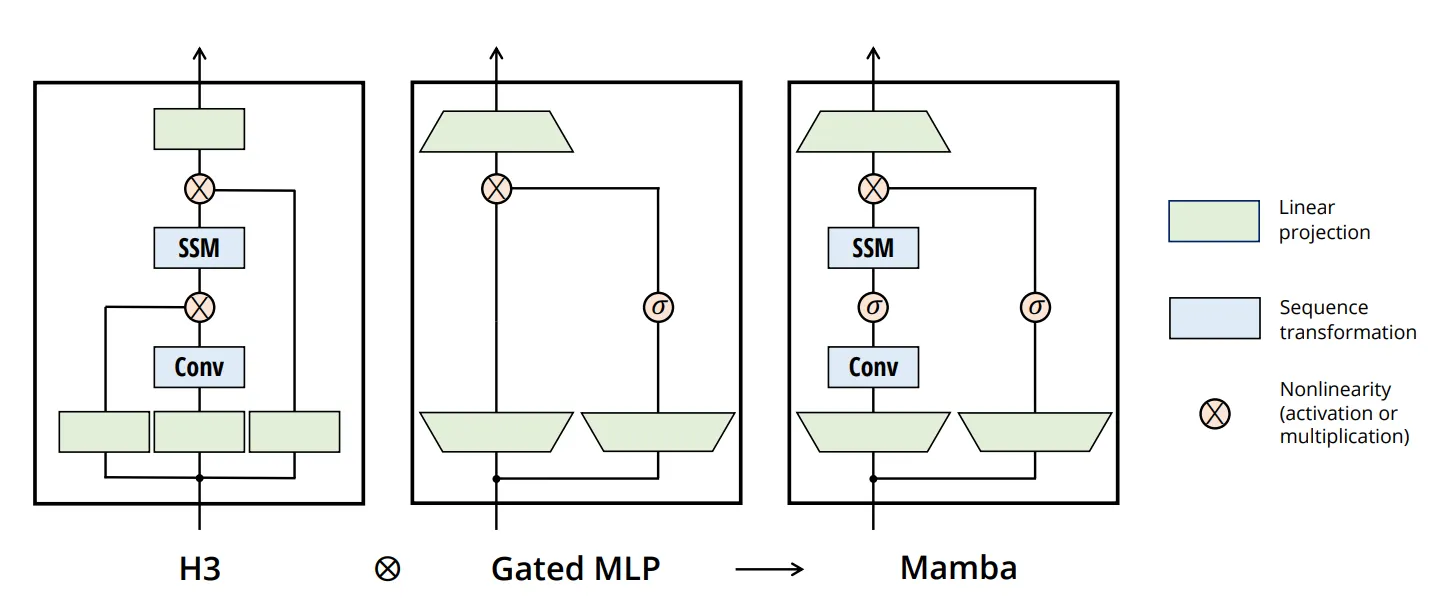
Mamba 架构示意图

在架构上，Mamba 结合了前序工作和 Gated MLP。在 SSM 变换前做了一个局部的 Casual conv，剩下的话就是让 FFN 包在外面了。

我们从 query-key attetnion 的视角来看一下 Mamba 的 SSM 在做什么。将 Mamba 输入 xtx_t 的每个维度 dd 看做 attention 中独立的 head，令

qt=WCxt∈RD,kt=WBxt∈RD,vt=(xt)d∈Rq_t = W_C x_t \in \R^D, k_t = W_Bx_t \in \R^D, v_t = (x_t)_d \in \R

这个 head 中，对于时间步 tt 的输出可看做：

yt=qtTht=qtT∑i=1t(∏j=i+1tAˉi)k~iviT\begin{aligned} y_t = q_t^T h_t = q_t^T \sum_{i=1}^t \left (\prod_{j=i+1}^{t} \bar A_i \right) \tilde k_i v_i^T \end{aligned}

其中 k~i=(ΔAi)−1(eΔAi−I)Δki∈RD\tilde k_i = (\Delta A_i)^{-1}(e^{\Delta A_i} -I)\Delta k_i \in \R^D。其实 query-key attention 的视角来看 mamba 的问题，感觉还是挺明显的，一个是它的 value dim 只有 1，另一个是它不同的 head 的 query 完全一样，它不同 head 间的 value 仅需要通过和某个向量做 Hadamard 积就可以转换。

Mamba-2

Mamba-2 主要的改进是由于 Mamba 的并行扫描对 GPU 的利用率仍然不如矩阵乘法。因此 Mamba-2 为了使用更多的矩阵乘法运算，将 head 的数量从 DD 削减到 Transformer 常用的一个维度。除此之外对 State Space Model，稍作修改，把它从输入 R\R 改为到 R1×P\R^{1\times P} 的（其中 PP 为 head dim）。

h′(t)=ath(t)+BTu(t)y(t)=Ch(t)\begin{aligned} \mathbf h'(t) &= a_t \mathbf h(t) +B^T\mathbf u(t) \\ \mathbf y(t) &= C \mathbf h(t) \end{aligned}

其中 B,C∈R1×N,h(t)∈RN×PB, C\in \R^{1\times N}, \mathbf h(t)\in \R^{N\times P}。其实等价于将每一维用相同的参数 (A,B,C)(A, B, C) 看度看做一个 SSM。所以其实离散化的过程几乎完全一样。

我们用 query-key attention 的方式重写一下：

qt=Ct=WCxt,kt=Bˉt=at−1(eΔat−1)WBxt,vt=xt\begin{aligned} q_t &= C_t = W_Cx_t, \\ k_t &= \bar B_t = a_t^{-1}(e^{\Delta a_t}-1)W_Bx_t, \\ v_t &= x_t \end{aligned}

中间省去的 ∏iai\prod_i a_i 可以看做是与另一个矩阵 LL 做 Hadamard 积：

Y=(L⊙QKT)VLij={∏k=j+1iak,i>j1,i=j0,i<j\begin{aligned} Y &= (L\odot QK^T)V \\ L_{ij} &= \begin{cases} \prod_{k=j+1}^i a_k & ,i>j\\ 1 &,i=j \\ 0 &,i<j \end{cases} \end{aligned}

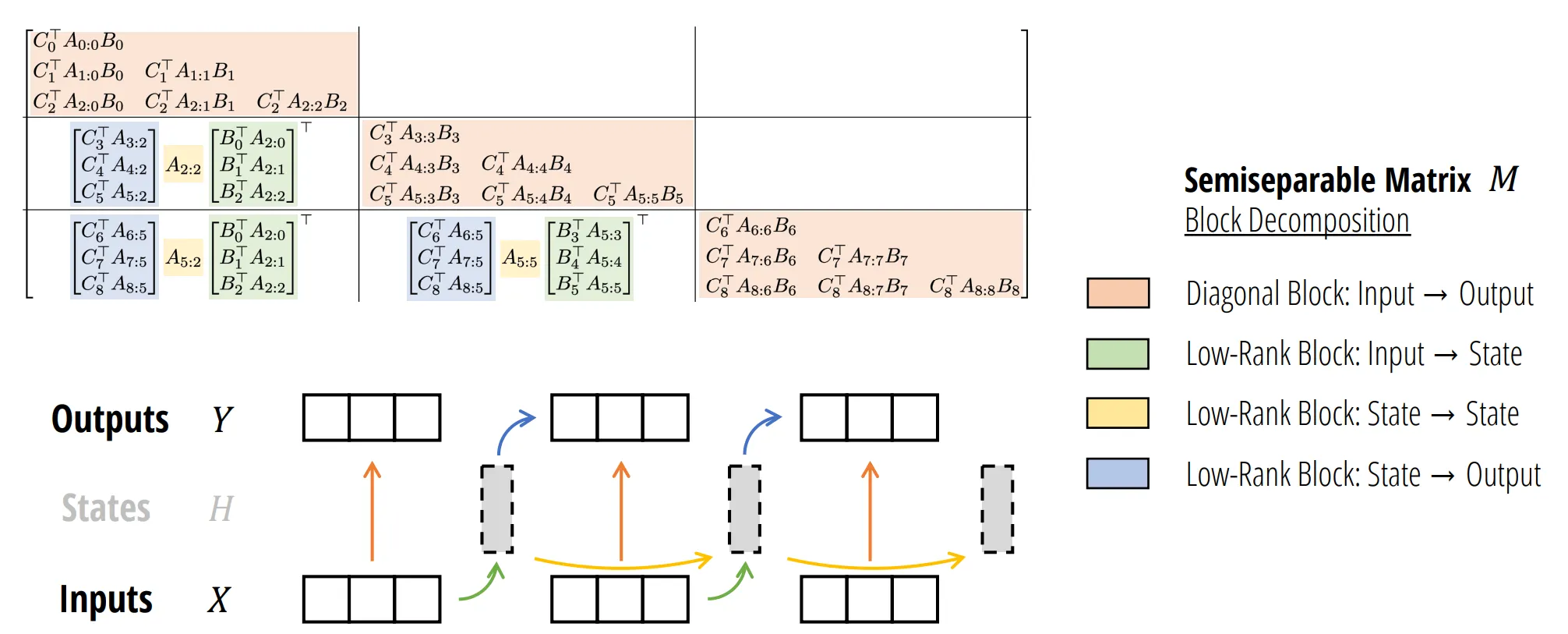
为了能高效训练，Mamba-2 结合分块，对于块内采用矩阵乘法进行计算，对于块间仍然采用并行扫描，但是由于并行扫描的序列长度减少了 chunk size 倍，因此效率更高。

Mamba-2 的分块并行扫描算法过程示意图

Mamba-3

Mamba-3 主要从 3 个方面进行改进 Mamba-2。

Trapezoidal Discretization

在 Mamba 和 Mamba-2 中，采用 Euler 积分，用右端的函数值近似为一个矩形，这在一个时间步内的积分会有 O(Δ2)O(\Delta^2) 的误差。在 Mamba-3 中则是采用推广的 Trapezoidal 积分，用积分两端的结果进行线性插值：

hk=eΔkAkhk−1+eAtk∫tk−1tke−AτB(τ)u(τ)dτ=eΔkAkhk−1+（1−λk)ΔkeΔkAkBk−1uk−1+λkBkuk\begin{aligned} h_k&=e^{\Delta_k A_k} h_{k-1} + e^{At_k}\int_{t_{k-1}}^{t_{k}} e^{-A\tau }B(\tau)u(\tau) \text d \tau \\ &= e^{\Delta_k A_k} h_{k-1} + （1- \lambda_k )\Delta_k e^{\Delta_k A_k}B_{k-1}u_{k-1} + \lambda_k B_ku_k \end{aligned}

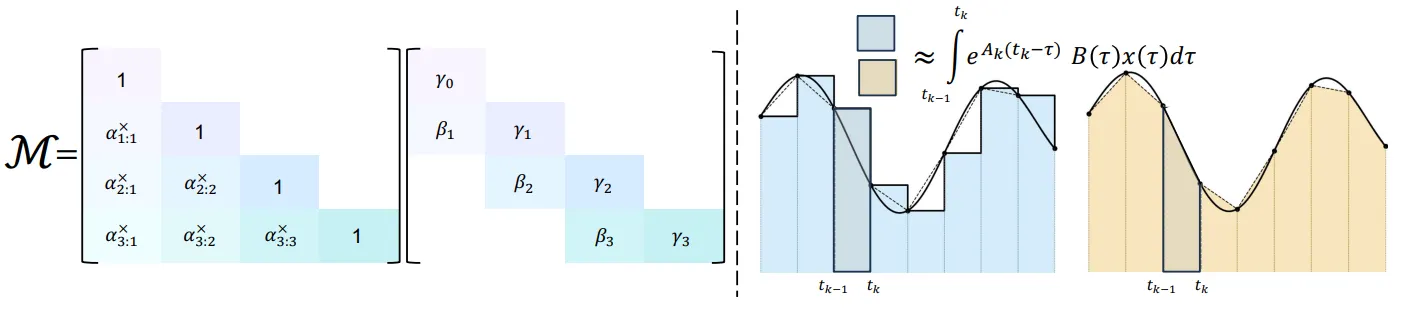
Euler 离散化和 Trapezoidal 离散化的差异

它对结构权重矩阵 LL 的影响相当于乘上了一个特殊的矩阵：

[γ0(γ0α1+β1)α2(γ0α1+β1)⋮⋱αT⋯2(γ0α1+β1)⋯γT]=[1α11α2α1⋮⋱αT⋯1⋯1][γ0β10γ2⋮⋱0⋯γT].\begin{bmatrix}\gamma_0 \\(\gamma_0\alpha_1+\beta_1) \\\alpha_2(\gamma_0\alpha_1+\beta_1) \\\vdots & & \ddots \\\alpha_{T\cdots2}(\gamma_0\alpha_1+\beta_1) & & \cdots & \gamma_T\end{bmatrix}=\begin{bmatrix}1 \\\alpha_1 & 1 \\\alpha_2\alpha_1 \\\vdots & & \ddots \\\alpha_{T\cdots1} & & \cdots & 1\end{bmatrix}\begin{bmatrix}\gamma_0 \\\beta_1 \\0 & \gamma_2 \\\vdots & & \ddots \\0 & & \cdots & \gamma_T\end{bmatrix}.

Complex-Valued SSMs

在 Mamba 以及 Mamba-2 中，SSM 模型中的 AA 采用实对角矩阵，这样不能表示复数的特征值。为了解决这一问题，Mamba-3 将 SSM 推广到复数域：

h˙(t)=Diag(A(t)+iθ(t))h(t)+(B(t)+iB^(t))x(t),y(t)=Re((C(t)+iC^(t))⊤h(t)),\begin{aligned} & \dot{\boldsymbol{h}}(t)=\mathrm{Diag}\left(A(t)+i\boldsymbol{\theta}(t)\right)\boldsymbol{h}(t)+\left(\mathbf{B}(t)+i\hat{\mathbf{B}}(t)\right)x(t), \\ & y(t)=\mathrm{Re}\left(\left(\mathbf{C}(t)+i\hat{\mathbf{C}}(t)\right)^\top\boldsymbol{h}(t)\right),\end{aligned}

其中 h(t)∈CN/2,θ(t),B(t),B^(t),C(t),C^(t)∈RN/2\boldsymbol{h}(t)\in\mathbb{C}^{N/2},\boldsymbol{\theta}(t),\mathbf{B}(t),\hat{\mathbf{B}}(t),\mathbf{C}(t),\hat{\mathbf{C}}(t)\in\mathbb{R}^{N/2}，x(t),A(t)∈Rx(t),A(t)\in\mathbb{R}。可以证明在 Euler 离散化下有

ht=eΔtAtRtht−1+ΔtBtxt,yt=Ct⊤ht\begin{aligned} \boldsymbol{h}_t&{=}e^{\Delta_tA_t}\mathbf{R}_t\boldsymbol{h}_{t-1}{+}\Delta_t\mathbf{B}_tx_t, \\ y_t&{=}\mathbf{C}_t^\top\boldsymbol{h}_t \end{aligned}

其中 Bt=[BtB^t]∈RN,Ct=[Ct−C^t]∈RN\mathbf{B}_t=\begin{bmatrix}\mathbf{B}_t \\\hat{\mathbf{B}}_t\end{bmatrix}\in\mathbb{R}^N,\quad\mathbf{C}_t=\begin{bmatrix}\mathbf{C}_t \\-\hat{\mathbf{C}}_t\end{bmatrix}\in\mathbb{R}^N。以及旋转矩阵：

Rt=Block({R(Δtθt[i])}i=1N/2)∈RN×N,R(Θ)=[cos⁡(Θ)−sin⁡(Θ)sin⁡(Θ)cos⁡(Θ)]\mathbf{R}_{t}=Block\left(\{R(\Delta_{t}\boldsymbol{\theta}_{\boldsymbol{t}}[i])\}_{i=1}^{N/2}\right){\in}\mathbb{R}^{N\times N}, R( \Theta)=\begin{bmatrix}\operatorname{cos}(\Theta) & -\operatorname{sin}(\Theta) \\\operatorname{sin}(\Theta) & \operatorname{cos}(\Theta)\end{bmatrix}

对于 Rt\mathbf R_t 的计算，可以采用和 RoPE 相同的 Trick 将其拆成两段前缀积的乘积，分到 query 和 key 的计算里面：

ht=eΔtAtht−1+(∏i=0tRi⊤)Btxt,yt=((∏i=0tRi⊤)Ct)⊤ht\begin{aligned} \boldsymbol{h}_t=e^{\Delta_tA_t}\boldsymbol{h}_{t-1}+(\prod_{i=0}^t\mathbf{R}_i^\top)\mathbf{B}_tx_t,\quad\boldsymbol{y}_t=\left((\prod_{i=0}^t\mathbf{R}_i^\top)\mathbf{C}_t\right)^\top\boldsymbol{h}_t \end{aligned}

Multi-Input, Multi-Output

单输入单输出和多输入多输出的算术强度对比

在不改变的参数情况下，增加隐藏层的维度，然后根据原来的维度分为 rr 个组，每个组采用相同的参数独立计算。由于解码时的算术强度增加，从 Memory-bound 的操作变为了 Compute-bound，所以这样的改变不会显著增加 decode 的时间，但是能够提升模型的效果。

Architecture

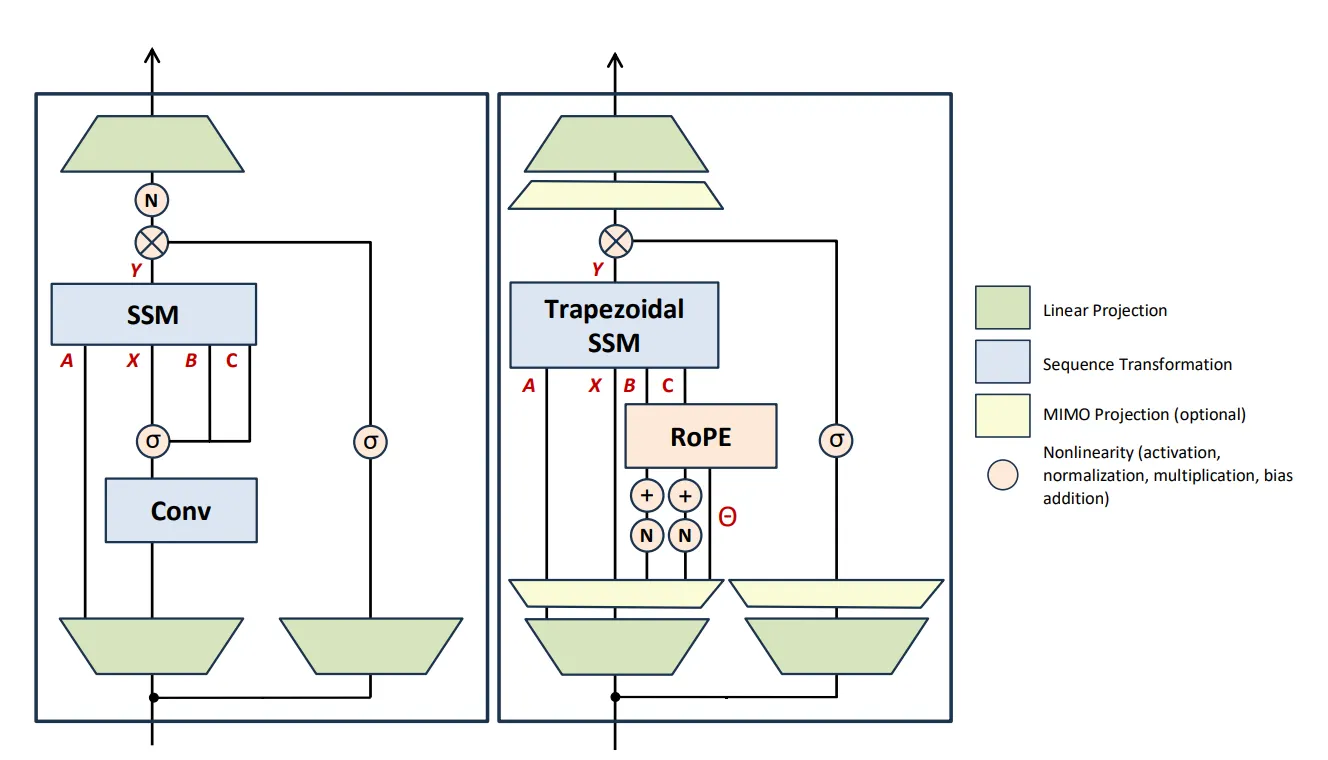
Mamba-3 和先前 Mamba 系列的架构对比

左图为 Mamba，右图为 Mamba-3。一个是移除了 Conv1d，另一个是在计算 B,CB, C 时加入了归一化和 RoPE。以及新增了额外的 MIMO 投影的模块。