Deep & Cross Network 系列速览

深度交叉网络（Deep & Cross Network）是推荐系统中很常见的一类模型，通过引入 Cross 网络来实现特征交叉，增强模型的表达能力。本文将快速介绍 DCN 三部曲以及其中两种变体 EDCN 和 GDCN。

粥的邀月的名片实在是太好看了，可惜不知道哪位老师画的。

DCN

对于线性模型 $y = w^Tx + b$ 的拟合能力显然不足，它没有考虑到不同领域之间的特征的交互的关系，为了增强它，考虑加入 $\sum_i \sum_j w_{ij} x_{i}x_j$ 等项，即因子分解机系列算法的想法。这个想法可以继续扩展：即增加 3 次项等更高次项。

为了避免去做 task-specific 的特征工程，作者考虑设计一个特定的网络结构去实现上面特征交叉加入高阶项的过程。作者考虑去用 $\mathbf{x}_0 \mathbf{x}_l^T$ 去增加最终表达式的 degree，同时为其增加一个权重 $\mathbf{w}_l$ 将其的维度从 $d\times d$ 变回 $d$。额外加入偏置项和残差连接得到了 Cross 网络部分的表达式：

$$\mathbf{x}_{l+1}=\mathbf{x}_0 \mathbf{x}_l^T \mathbf{w}_l+\mathbf{b}_l+\mathbf{x}_l=f\left(\mathbf{x}_l, \mathbf{w}_l, \mathbf{b}_l\right)+\mathbf{x}_l$$

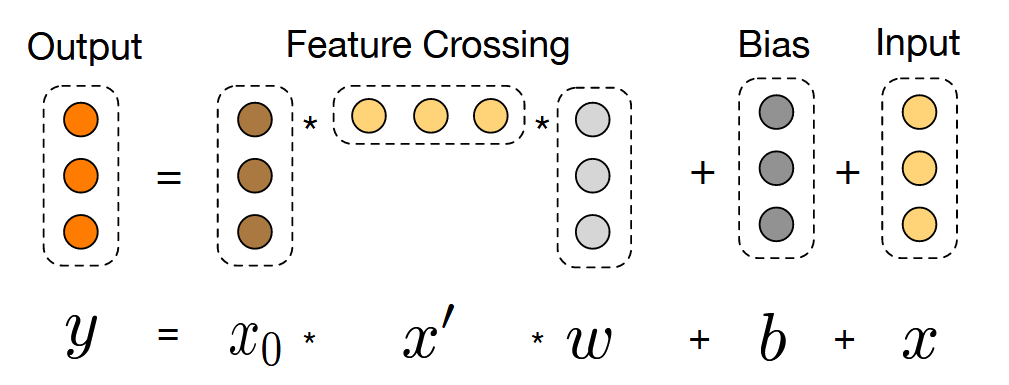
将 Cross 网络和传统的深度神经网络（DNN）捕获的隐特征进行结合，得到了最终的 DCN 网络：

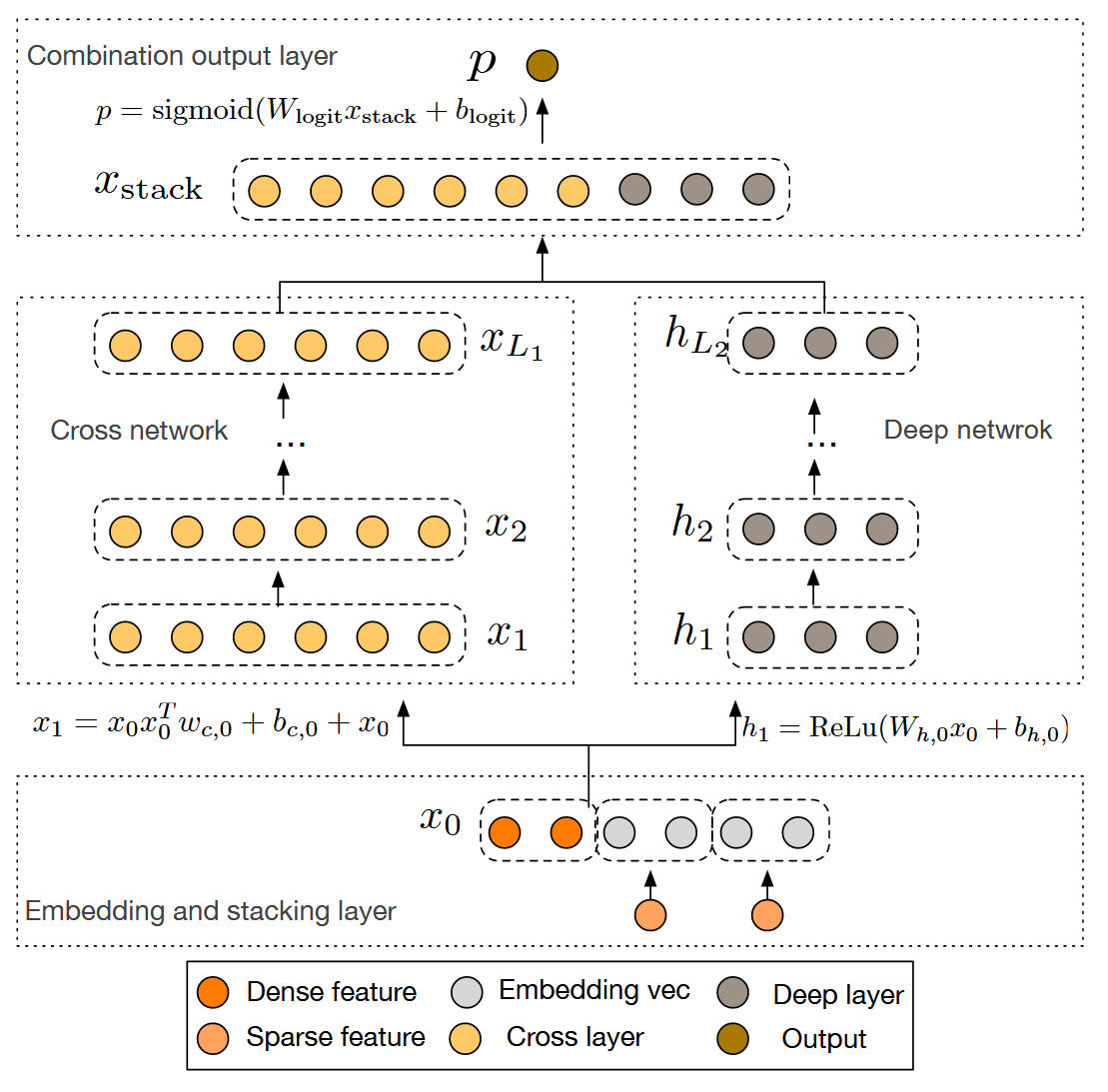
DCN-v2

工业界中 LTR（Learning to rank） 模型已经由线性回归模型、因子分解机模型逐步迁移至深度神经网络。但是一些研究表明 DNN 去毕竟二阶以及更高阶特征交叉时非常低效。而增大模型则会增大延时，这对工业界来说难以接受。

DCN 能够更好地去学习高阶特征交叉，但是由于 Cross 网络每层参数只有 $O(d)$，导致 Cross 网络部分表达能力很有限。而 DNN 部分每层的参数为 $O(d^2)$，与 Cross 网络差距较大，而这一差距在更大的数据集上被放大了。

为了增强 Cross 部分的表达能力，对计算公式做一个简单修改，将用向量来作为权重变为用矩阵来作为权重，赋予交叉的过程更大的自由度：

$$\mathrm{x}_{l+1}=\mathrm{x}_0 \odot\left(W_l \mathrm{x}_l+\mathrm{b}_l\right)+\mathrm{x}_l$$

为了和已有的模型进行对比，除了之前 Parallel 的 DCN 结构，额外提了一个 Stacked 的结构。

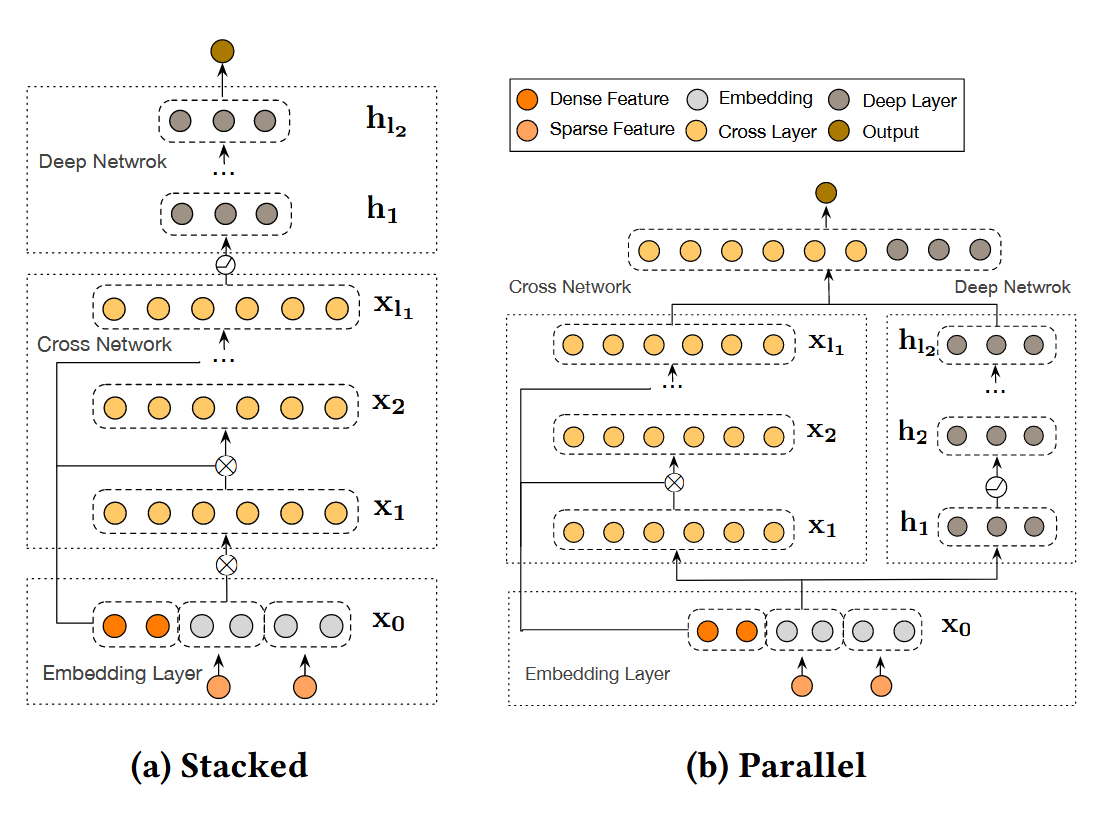
效率优化

作者尝试利用低秩方法去优化模型的效率和参数。作者观察了在 Cross 网络中习得的参数的奇异值的分布，发现将特征值排序后，特征值衰减地非常快。因此可以考虑只保留最大的 $k$ 个参数，然后我们去近似 $U \Sigma V^T$，其中 $U\in \R^{d\times k}, V\in \R ^{d\times k}$。不过我们可以直接学习 $U\Sigma$，因此简化一些得到了下面的式子：

$$\mathrm{x}_{l+1}=\mathrm{x}_0\odot\left(U_l\left(V_l^\top\mathrm{x}_i\right)+\mathrm{b}_l\right)+\mathrm{x}_i$$

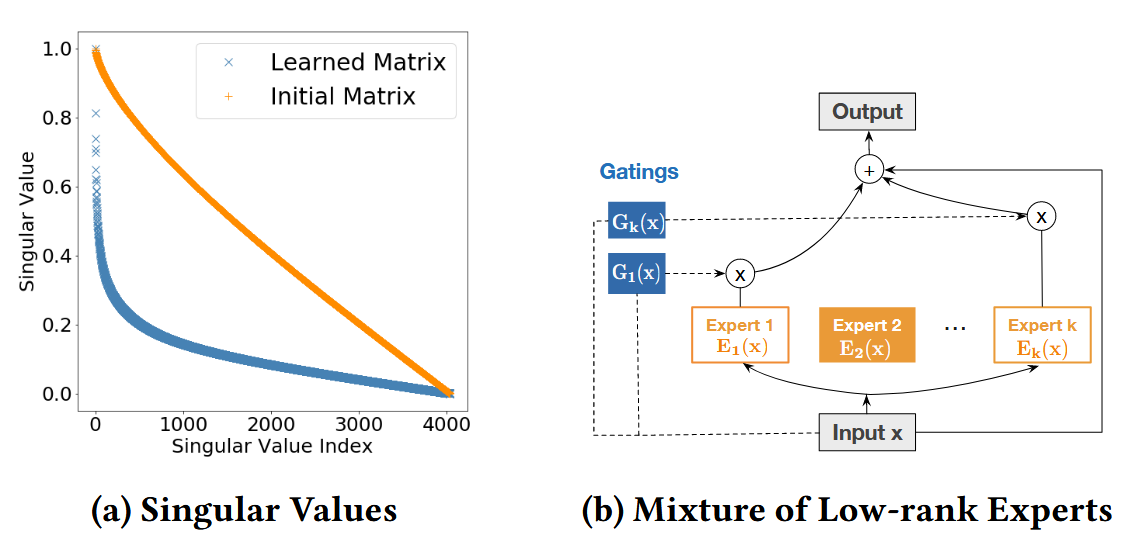
作者对这个式子给出两种看法：

1. 我们在子空间 $\R^k$ 中学习特征交叉。
2. 我们将 $\mathbf x_i$ 投影到子空间，然后再投影回 $\R^d$。

由此作者提出了两种提升效果的思路：

1. 利用 MoE 去混合一些低秩模型

   $$\begin{aligned} \mathrm{x}_{l+1} & =\sum_{i=1}^K G_i\left(\mathrm{x}_l\right) E_i\left(\mathrm{x}_l\right)+\mathrm{x}_l \\ E_i\left(\mathrm{x}_l\right) & =\mathrm{x}_0 \odot\left(U_l^i\left(V_l^{i \top} \mathrm{x}_l\right)+\mathrm{b}_l\right) \end{aligned}$$

2. 利用投影的低秩空间 —— 增加非线性变换

   $$E_i\left(\mathrm{x}_l\right)=\mathrm{x}_0 \odot\left(U_l^i \cdot g\left(C_l^i \cdot g\left(V_l^{i \top} \mathrm{x}_l\right)\right)+\mathrm{b}_l\right)$$

   其中 $g$ 为非线性变换，$C_l^i \in \R^{k\times k}$ 为 $\R^d$ 中的一个线性变换。

EDCN

作者指出 DCN 系列中可能存在的问题：

• 每一层的隐状态的参数没有充分交互：cross 和 deep 网络的参数是独立的
• cross 和 deep 网络享有相同的输入特征，但是不同的特征可能适配不同的特征交互的方式，因此对于每个网络只使用部分选择过的特征的方法可能能得到更好的效果

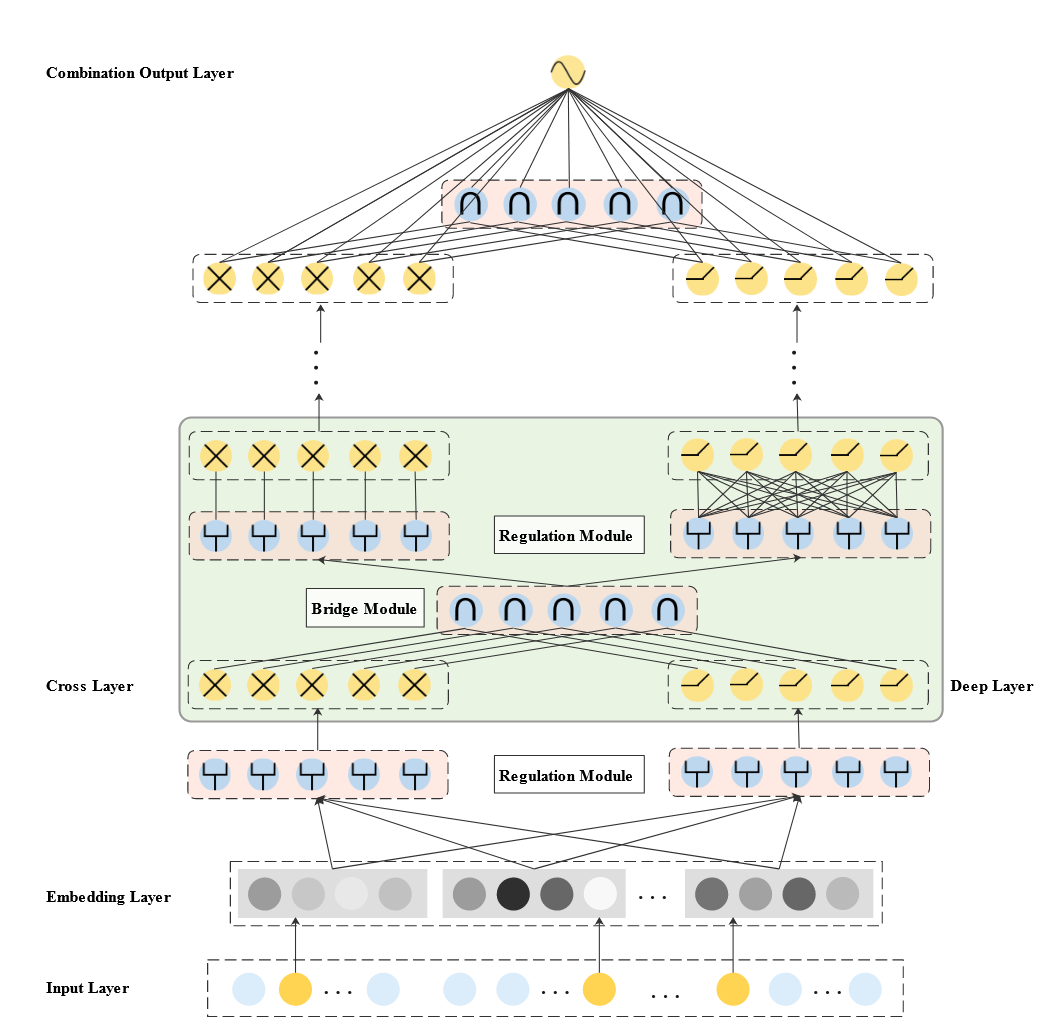
为了改善这两个问题，作者分别提出 bridge module 用户融合特征以及 regulation module 去差异化 cross 和 deep 网络的输入。

Bridge Module

Bridge module 用于连接并融合 cross 和 deep 网络的隐状态，假设上层 cross 和 deep 网络的输出分别为 $\mathbf{x}_l$ 和 $\mathbf{h}_l$，有 4 种常用的连接方法：

• 逐位相加
• Hadamard 积
• 连接之后使用线性层和激活函数恢复维度
• 使用自注意力去为 $\mathbf{x}_l$ 和 $\mathbf{h}_l$ 计算权重，然后加权和 $\mathbf{f}_l=a_l^x \mathbf{x}_l \oplus a_l^h \mathbf{h}_l$

通过消融实验，作者发现使用 Hadamard 积效果比较好。

Regulation Module

对于 cross 和 deep 分别学习一个 Gate 向量，然后结合参数温度 $\tau$ 进行 Softmax 归一化。

$$\widehat{\mathbf{g}}_i^b=\frac{e^{\frac1\tau\mathbf{g}_i^b}}{\sum_{j=1}^fe^{\frac1\tau\mathbf{g}_j^b}}$$

接着通过 Hadamard 积计算实际输入的内容：

$$\mathrm{E}^b=\widehat{\mathrm{G}}^b\odot\mathrm{E}=[\widehat{\mathrm{g}}_1^b\mathbf{e}_1,\widehat{\mathrm{g}}_2^b\mathbf{e}_2,\cdots,\widehat{\mathrm{g}}_f^b\mathbf{e}_f].$$

Combination Output Layer

在最后一层，将三种网络（Cross、Deep 以及最后一层 Bridge 网络）的输出拼合到一起，再加上线性层输出。

GDCN

作者分析现有的模型，列出两点不足的地方：

• 很多现有的 sota 模型，当交互的阶数超过一定的时候（通常是三阶），表现会退化。作者认为的原因是高阶特征会带来许多噪声，而之前的模型去噪做的并不好。
• 现存的模型的嵌入层冗余度很高：对于每个领域的嵌入层，基于经验为其分配维度。

作者也基于 DCN-v2 的两种堆叠方式分别加入 Gate：

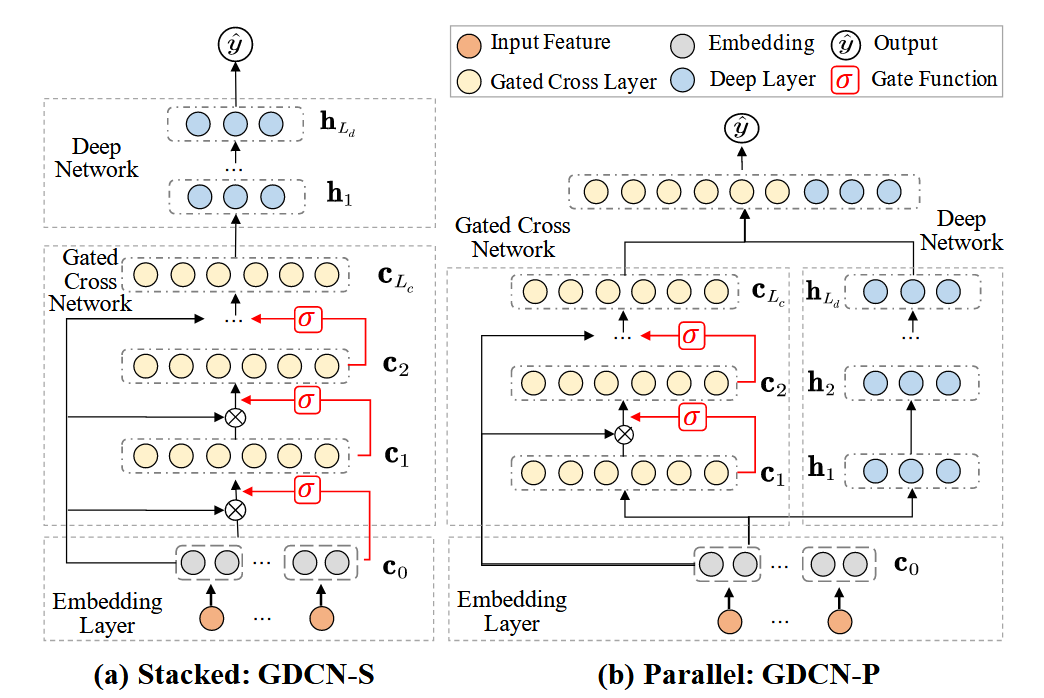
Gated Cross Network

用每层输入的特征 $\mathbf{c}_l$ 去生成一个 Gate 权重，用于过滤特征交互得到噪声。

$$\mathbf{c}_{l+1}= \underbrace{\mathbf{c}_0\odot\left(\mathbf{W}_l^{(c)}\times\mathbf{c}_l+\mathbf{b}_l\right)}_{F eature Crossing} \odot \quad \underbrace{\sigma\left(\mathbf{W}_l^{(g)}\times\mathbf{c}_l\right)}_{Inf ormation Gate}\quad+\mathbf{c}_l$$

Field-level Dimension Optimization

1. 首先使用对于每种特征使用充足的嵌入层大小来训练整个模型
2. 然后为每种特征的嵌入矩阵计算其奇异值，将其按大到小排序，通过为 $\frac{\sum_{i=1}^k \sigma_i^2}{\sum_{i=1}^n\sigma_i}$ 设定阈值来选择新的维度 $k$，或者设置 $T (0 < T < 1)$ ，保留所有大于等于 $T\sigma_1$ 的奇异值，由此来决定新的维度。
3. 根据上面的结果重新训练一个新的模型

DCN-v3

DCN-v3 改进的主要的想法：

• 大多数显式特征交叉网络的效果不如深度网络
• 高阶交互特征会带来很多的噪声，目前过滤噪声的方式比较低效
• 不充分的监督学习信号

Cross Network

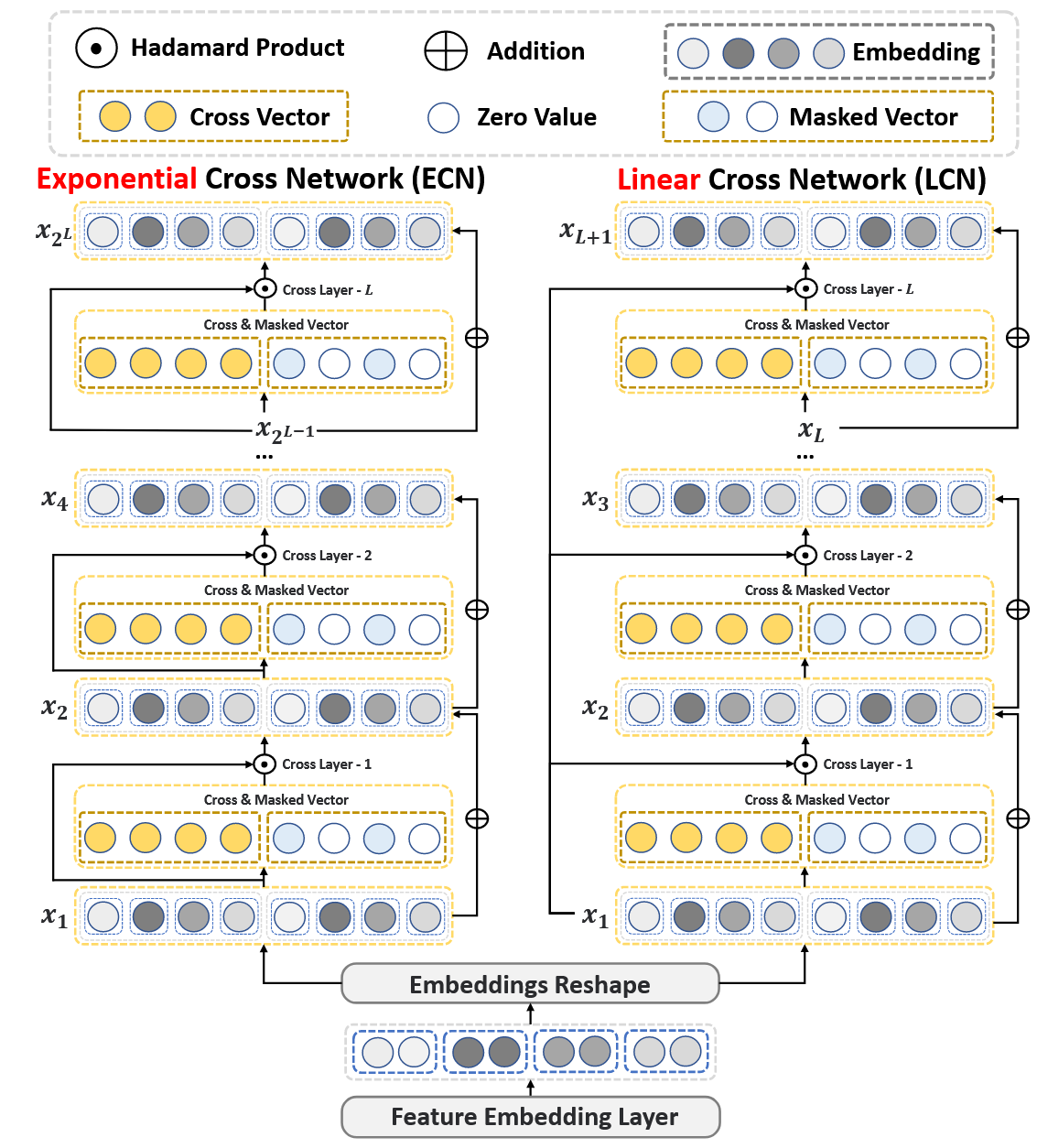
DCN-v3 提供了两种 cross 网络：指数交叉网络和线性交叉网络。为了过滤高阶噪声，额外设计了一个 mask：

$$\begin{aligned}\mathbf{c}_l&=\mathbf{W}_l\mathbf{x}_l+\mathbf{b}_l,\\\mathbf{x}_{l+1}&=\mathbf{x}_1\odot[\mathbf{c}_l\mid\mid\mathsf{Mask}(\mathbf{c}_l)]+\mathbf{x}_l\end{aligned}$$

其中 $\mid\mid$ 表示拼接操作。其中 $W_l$ 将 $x_l$ 投影到 $\frac{d}{2}$ 维空间中。其中 Mask 操作如下：

$$\mathsf{Mask}(\mathbf{c}_l)=\mathbf{c}_l\odot\max(0,\mathrm{~LN}(\mathbf{c}_l))$$

其中 $\mathrm{LN}(\cdot)$ 表示 LayerNorm 操作。

Embedding & Reshape Layer

为了对应之后结构，每种特征的 Embedding 将会提供两种，最后以下面的方式拼合到一起：

$$\mathbf{x_1}=\begin{bmatrix}\mathbf{e}_{1,a},\cdots,\mathbf{e}_{f,a},\mathbf{e}_{1,b},\cdots,\mathbf{e}_{f,b}\end{bmatrix}\in\mathbb{R}^D$$

这样做的目的是让前半部分作为直接计算的值，而另一部分用于生成相应的 mask。

Loss

最终通过对 ECN 和 LCN 的结果取均值的方式，对其结果进行融合：

$$\begin{aligned}\hat{y}_{D}&=\sigma(\mathbf{W}_D\mathbf{x}_{2^L}+\mathbf{b}_D),\\\hat{y}_{S}&=\sigma(\mathbf{W}_S\mathbf{x}_{L+1}+\mathbf{b}_S),\\\hat{y}&=\mathsf{Mean}(\hat{y}_D,\hat{y}_S),\end{aligned}$$

对于 Loss 不仅计算 $\hat y$ ，分别将两个网络的信息也加入考虑：

$$\begin{gathered} \mathcal{L} =-\frac{1}{N}\sum_{i=1}^{N}\left(y_{i}\log\left(\hat{y}_{i}\right)+\left(1-y_{i}\right)\log\left(1-\hat{y}_{i}\right)\right), \\ \mathcal{L}_D =-\frac1N\sum_{i=1}^N\left(y_i\log\left(\hat{y}_{D,i}\right)+\left(1-y_i\right)\log\left(1-\hat{y}_{D,i}\right)\right), \\ \mathcal{L}_S =-\frac1N\sum_{i=1}^N\left(y_i\log\left(\hat{y}_{S,i}\right)+\left(1-y_i\right)\log\left(1-\hat{y}_{S,i}\right)\right), \end{gathered}$$

为了为两个子网络提供正确的监督信号，为其分别赋予权重 $\mathbf{w}_D= \max(0, \mathcal L_D - \mathcal L ) $ 和 $\mathbf w _S$，得到最终的损失的式子：

$$\mathcal{L}_{\mathrm{Tri}}=\mathcal{L}+\mathbf{w}_D\cdot\mathcal{L}_D+\mathbf{w}_S\cdot\mathcal{L}_S$$

这样去做的原因是当如果只使用最终的损失，子网络一般仍然还可以继续进行优化，因此引入辅助的损失来帮助进一步优化子网络。相关的证明见另一篇论文。

References

1. Deep & Cross Network for Ad Click Predictions, https://arxiv.org/abs/1708.05123
2. DCN V2: Improved Deep & Cross Network and Practical Lessons for Web-scale Learning to Rank Systems, https://arxiv.org/abs/2008.13535
3. DCNv3: Towards Next Generation Deep Cross Network for Click-Through Rate Prediction, https://arxiv.org/abs/2407.13349
4. Enhancing Explicit and Implicit Feature Interactions via Information Sharing for Parallel Deep CTR Models, https://dlp-kdd.github.io/assets/pdf/DLP-KDD_2021_paper_12.pdf
5. Towards Deeper, Lighter and Interpretable Cross Network for CTR Prediction, https://arxiv.org/abs/2311.04635