光子映射系列速览：PM、PPM、SPPM

有效地实现全局光照的模拟是计算机图形学中一个经典的问题，在 1998 年 Veach 的博士论文中给出了无偏 Monte-Carlo 模拟的 Path Tracing 算法，但是路径追踪算法在模拟焦散时并不准确。但 Monte-Carlo 的误差为 $O(n^{-1/2})$，增加采样点对最终渲染效果的提升始终有限。

焦散是指光线经过透明物体时，经过一次或多次折射和反射在漫反射表明形成的光影现象，例如下图这个水杯折射后光线在桌面上形成的图像：

为了简单，我们下面仅考虑三种材质：Lambertian 材质（完美的漫反射）、镜面材质（完美的镜面反射）、透明材质（只考虑折射）。渲染的物体的材质由这三种材质混合来表示。

Photon Mapping

光子映射的想法很简单：让光源发出若干个光子，光子可以被漫反射表面 “吸收“ 一部分，同时会被镜面物体反射，以及会穿过透明物体。我们用某个数据结构存储所有被 “吸收” 的光子位置等信息。接着我们从相机视角开始渲染图像：从相机发出 “光线”，这个 “光线” 和路径追踪的类似，我们希望估计这个方向上的 radiance，接着它会在镜面物体反射，以及会穿过透明物体，但是当它遇到一个漫反射物体的时候，由于漫反射物体会 “吸收” 一部分光子，我们可以借助这部分来估计此处会辐射出的 radiance。

先提一下后面的计算，在渲染方程中，我们实际是要计算：

$$L_o(x, \omega_o) = \int f_r(x, \omega_i\to \omega_o) L_i(x, \omega_i) |\cos \theta| \text d \omega_i$$

其中 $\theta$ 是 $\omega_i$ 和法向量 $n$ 的夹角。将辐射率 $L_i(x, \omega_i) = \frac{\text d^2 \Phi_i(x, w_i)}{\text d (A|\cos\theta|) \text d \omega_i}$ 代入可得：

$$L_o(x, \omega_o) = \int f_r(x, \omega_i\to \omega_o)\frac{\text d^2 \Phi_i(x, \omega_i)}{\text d A}$$

光子映射的前一部分就是希望去估计上式右侧的积分式子。$\text dA$ 可以看做是在 $x$ 附近取了一块面积元，$\text d^2 \Phi$ 可以看做是对光源在方向角和面积上分别进行微分，这个便是统计在光源的一个面积元上向一个很小的单位角（视为射线）辐射的通量（flux）。离散形式的话如大致就是：

$$L_o(x, \omega_o)\approx \sum_{j} f_{r}(x, \omega_j\to \omega _o) \frac{\Delta \Phi_j}{\Delta A}$$

其中 $j$ 是所有落在面积元 $\text d A$ 中的光子，$\omega_j$ 表示光子 $j$ 的入射方向。但是实际情况是不太可能有那么多光子来模拟在光源做了两次微分的结果，所以实际上是确定光源发射出光子的数量 $n_{emit}$，然后认为每个光子带有相同的能量。

因为实际表面很复杂，可能有一些面数特别多的模型，只取当前面上的光子的话，可能由于数量太少了没有办法准确估计，所以这里邻近的光子取 $x$ 的 $k$ 邻近或者半径为 $r$ 内的所有光子，然后用距离 $x$ 最远光子的距离 $r_{mx}$ 为半径作一个圆，作为面积元 $\Delta A$。我们可以使用 KDTree 来优化查找的过程。初步实现的渲染结果如下：

可以看见有非常多的光斑，这个是没有办法准确估计出 radiance 导致的。以及在墙角和物体边缘的过亮的情况，这个是因为通过上面方法估计 radiance 时，会将不属于该面的一些光子的贡献算进来：

Progressive Photon Mapping

如果想改善光子映射的效果，有一个必然的想法是发射更多的光子，但是更多的光子意味着，在存储全局光子的时候需要更多的内存。PPM 算法的想法是进行多轮的光子贴图，然后对光子贴图然后根据每一轮的光子贴图的结果更新估计的 radiance。

具体地来讲，PPM 首先会从相机的每个像素采样，然后做一次 path tracing，得到像素个数乘 spp （Samples Per Pixel，每像素采样数）个观察点，以及每个观察点的入射方向 $v_i$ 和由于中间反射和折射对能量的贡献系数 $\beta_i$。接着我们需要估计每个观察点向 $-v_i$ 方向辐射的 radiance。

对于第一次 photon mapping，每个观察点统计 $r_0$ 范围内的所有光子，统计它的数量 $n_1$ 以及这些向 $\omega_o$ 方向辐射的辐射强度（radiant intensity） $\tau_1 = \sum_p f_r(x_p, \omega_i^{(p)}, \omega_o) \Delta \Phi(x_p, \omega_i^{(p)})$。其中 $r_0$ 为参数，在算法进行前选定，$p$ 为某个范围内的光子，$\omega_i^{(p)}$ 表示它的入射方向。

对于后面的 photon mapping 的过程，我们希望结合之前的结果进行一个更准确的估计。一方面我们有了更多的光子，另一方面我们可以减少统计的半径来获得更精确的结果。所以我们希望在累积新的光子的同时减少统计的半径。假设在之前的过程中，当前观察点的观测半径为 $r_1$，累积到光子的数量 $n_1$，以及这些光子的辐射强度和 $\tau_1$，在当前这一轮 photon mapping 中，新累积到的光子的数量 $n_2$，以及通过反射向 $\omega_o$ 方向的辐射强度和 $\phi$。接着我们希望缩减统计半径，将 $r_1$ 减少为 $r_2$，使得这轮更新后实际只会新增 $\alpha n_2$ 个光子，在这个过程中，我们假设光子的密度是不会改变的。因此有：

$$\frac{n_1+n_2}{\pi r_1^2} = \frac{n_1 + \alpha n_2}{\pi r_2^2}$$

得：$r_2 = r_1\sqrt{\frac{n_1 + \alpha n_2}{n_1 + n_2}}$。接着假设光子的能量分布是均匀的，于是直接根据面积比修正缩减半径后的辐射强度：

$$\tau_2 = (\tau_1 + \phi)\frac{n_1 + \alpha n_2}{n_1 + n_2}$$

接着在多轮 photon mapping 过程执行结束后，我们用一个像素对应的所有观察点来估计它接受的辐射率。假设 $k$ 为现在进行的轮数，那么我们需要将累积的辐射强度除以 $k$，同时除以面积元的大小来估计辐射率：

$$L(x, \omega_o) = \frac{1}{n_{watch}} \sum_i \frac{\tau_{k}(x_i, \omega_o^{(i)})\beta_i}{k \pi r_k(x_i)}$$

其中 $\omega_o^{(i)}$ 表示第 $i$ 个观察点对应的出射方向。实现的效果如下，可以看见相比 Photon Mapping 算法效果有很大的提升：

Stochastic Progressive Photon Mapping

PPM 仍然有一个问题如果我渲染的图像比较大，并且 spp 取得很高，那么观测点会非常占用内存，SPPM 对 PPM 做出改进：不再维护一个庞大观察点图，而是在每一次 photon mapping 过程后重新采样观察点，并且我们直接维护这个像素累积的辐射率，并且认为同一个像素采样的观察点共享半径和累积辐射率。

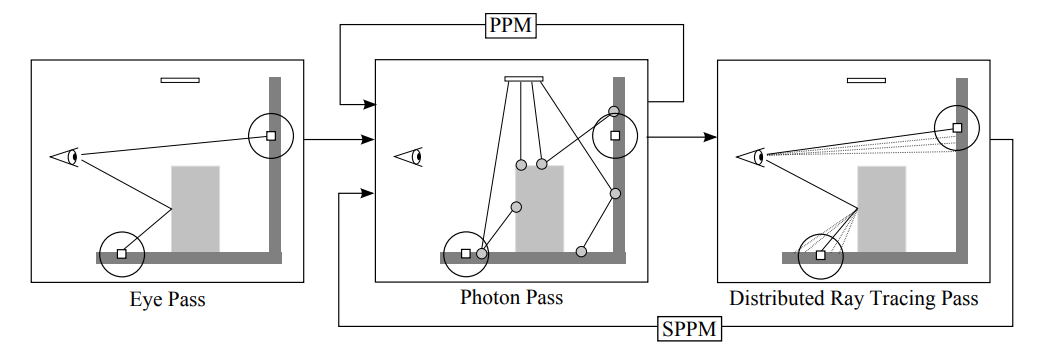
我这里实现的时候 累积辐射率 实际计算的是 在观察点上统计的辐射率 $L$ 乘贡献系数 $\beta$ 后在像素上累积的辐射率。在第 $k$ 轮 photon mapping 结束后，计算在像素上的累积辐射率 $L_k$，将 $\frac{L_k}{k}$ 累积到像素的颜色中，接着用 $n$ 轮的颜色的均值作为最终的像素颜色的估计值。

对于边界过亮的问题，通过直接屏蔽掉所在面法向和当前面法向夹角大于等于 $\frac{\pi}{2}$ 的光子，对于能量计算的方法又稍微调整了一下。我实现的能量计算的方法应该一直都不太正确，感觉主要是瞎调系数的算法糊效果。现在的渲染效果如下：

收敛过程大致可以参考一下下面这个 gif：