Diffusion Models 的想法是通过缓慢地将噪声加入数据,然后学习逆向扩散的过程,从而能从噪声中构建出所需要的样本。
设 x 0 x_0 x 0 x T x_T x T q q q p p p
前向扩散 ,逐步向图像中添加高斯噪声,设在 t − 1 t -1 t − 1 t t t β t \beta_t β t
x t = 1 − β t x t − 1 + β t ϵ ( ϵ ∼ N ( 0 , I ) ) x_t = \sqrt{1 - \beta_t} x_{t-1} +\sqrt{\beta_t}\epsilon\ (\epsilon \sim\mathcal N(\mathbf 0, \mathbf I))
x t = 1 − β t x t − 1 + β t ϵ ( ϵ ∼ N ( 0 , I ) )
逆向扩散 ,从某个存在噪声的时刻 x t 0 x_{t_0} x t 0 x 0 x_0 x 0
我们对 x t x_t x t α t = 1 − β t \alpha_t = 1 - \beta_t α t = 1 − β t
x t = 1 − β t x t − 1 + β t ϵ = α t x t − 1 + 1 − α t ϵ = α t α t − 1 x t − 2 + α t ( 1 − α t − 1 ) ϵ 1 + 1 − α t ϵ 2 \begin{aligned}
x_t &= \sqrt{1 - \beta_t} x_{t - 1} + \sqrt{\beta_t} \epsilon \\
&= \sqrt{\alpha_t} x_{t - 1} + \sqrt{1 - \alpha_t} \epsilon \\
&= \sqrt{\alpha_t\alpha_{t-1}} x_{t-2} + \sqrt{\alpha_t(1 - \alpha_{t-1})}\epsilon_1 + \sqrt{1 - \alpha_t} \epsilon_2
\end{aligned}
x t = 1 − β t x t − 1 + β t ϵ = α t x t − 1 + 1 − α t ϵ = α t α t − 1 x t − 2 + α t ( 1 − α t − 1 ) ϵ 1 + 1 − α t ϵ 2
由于 α t ( 1 − α t − 1 ) ϵ 1 ∼ N ( 0 , α t ( 1 − α t − 1 ) I ) \sqrt{\alpha_t(1 - \alpha_{t-1})}\epsilon_1 \sim \mathcal N(\mathbf 0, \alpha_t(1 - \alpha_{t-1})\mathbf I) α t ( 1 − α t − 1 ) ϵ 1 ∼ N ( 0 , α t ( 1 − α t − 1 ) I ) 1 − α t ϵ 2 ∼ N ( 0 , ( 1 − α t ) I ) \sqrt{1 - \alpha_t} \epsilon_2 \sim \mathcal N(\mathbf 0, (1 - \alpha_t)\mathbf I) 1 − α t ϵ 2 ∼ N ( 0 , ( 1 − α t ) I ) α t ( 1 − α t − 1 ) ϵ 1 + 1 − α t ϵ 2 ∼ N ( 0 , ( 1 − α t α t − 1 ) I ) \sqrt{\alpha_t(1 - \alpha_{t-1})}\epsilon_1 + \sqrt{1 - \alpha_t} \epsilon_2\sim \mathcal N(\mathbf 0, (1 - \alpha_t\alpha_{t-1}) \mathbf I) α t ( 1 − α t − 1 ) ϵ 1 + 1 − α t ϵ 2 ∼ N ( 0 , ( 1 − α t α t − 1 ) I )
所以有 x t = α t α t − 1 x t − 2 + 1 − α t α t − 1 ϵ x_t = \sqrt{\alpha_t\alpha_{t - 1}} x_{t - 2} + \sqrt{1 - \alpha_t\alpha_{t-1}} \epsilon x t = α t α t − 1 x t − 2 + 1 − α t α t − 1 ϵ x t = ∏ i = 1 t α i x 0 + 1 − ∏ i = 1 t α i ϵ x_t = \sqrt{\prod_{i=1}^t \alpha_i} x_0 +\sqrt{1 - \prod_{i=1}^t\alpha_i} \epsilon x t = ∏ i = 1 t α i x 0 + 1 − ∏ i = 1 t α i ϵ
令 α t ˉ = ∏ i = 1 t α i \bar{\alpha_t} = \prod_{i = 1}^t \alpha_i α t ˉ = ∏ i = 1 t α i
x t = α t ˉ x 0 + 1 − α ˉ t ϵ \begin{aligned}
x_t = \sqrt{\bar{\alpha_t}} x_0 + \sqrt{1 - \bar \alpha_t} \epsilon
\end{aligned}
x t = α t ˉ x 0 + 1 − α ˉ t ϵ
随着时间不断推移,α t ˉ → 0 \bar{\alpha_t} \to 0 α t ˉ → 0 x ∞ ∼ N ( 0 , I ) x_{\infty} \sim N(\mathbf 0, \mathbf I) x ∞ ∼ N ( 0 , I )
现在我们希望计算从 x t x_{t } x t x t − 1 x_{t-1} x t − 1 q ( x t − 1 ∣ x t ) q(x_{t - 1} \mid x_t) q ( x t − 1 ∣ x t ) x 0 x_0 x 0 x 0 x_0 x 0
q ( x t − 1 ∣ x t , x 0 ) = q ( x t ∣ x t − 1 , x 0 ) q ( x t − 1 ∣ x 0 ) q ( x t ∣ x 0 ) = 1 2 π ( 1 − α t ) exp ( − ∥ x t − α t x t − 1 ∥ 2 2 ( 1 − α t ) ) ⋅ 1 2 π ( 1 − α ˉ t − 1 ) exp ( − ∥ x t − 1 − α ˉ t − 1 x 0 ∥ 2 2 ( 1 − α ˉ t − 1 ) ) 1 2 π ( 1 − α t ˉ ) exp ( − ∥ x t − α t ˉ x 0 ∥ 2 2 ( 1 − α t ˉ ) ) ∝ exp ( − ∥ x t − α t x t − 1 ∥ 2 2 ( 1 − α t ) − ∥ x t − 1 − α ˉ t − 1 x 0 ∥ 2 2 ( 1 − α ˉ t − 1 ) + ∥ x t − α t ˉ x 0 ∥ 2 2 ( 1 − α t ˉ ) ) = exp ( − 1 2 [ ( α t β t + 1 1 − α ˉ t − 1 ) ∥ x t − 1 ∥ 2 − ( 2 α t β t x t + 2 α ˉ t − 1 1 − α ˉ t − 1 x 0 ) x t − 1 + C ( x t , x 0 ) ] ) \begin{aligned}
q(x_{t - 1} \mid x_t, x_0) &= \frac{q(x_{t}\mid x_{t-1}, x_0) q(x_{t-1}\mid x_0)}{q(x_{t} \mid x_0)} \\
&= \frac
{
\frac{1}{\sqrt{2\pi(1 - \alpha_t)}}\exp(-\frac{\|x_t - \sqrt{\alpha_t}x_{t-1}\|^2}{2(1 - \alpha_t)})
\cdot
\frac{1}{\sqrt{2\pi(1 - \bar{\alpha}_{t-1})}}\exp(-\frac{\|x_{t-1} - \sqrt{\bar{\alpha}_{t-1}}x_{0}\|^2}{2(1 - \bar{\alpha}_{t-1})})
}
{\frac{1}{\sqrt{2\pi(1 - \bar{\alpha_{t}})}}\exp(-\frac{\|x_{t} - \sqrt{\bar{\alpha_{t}}}x_{0}\|^2}{2(1 - \bar{\alpha_{t}})})} \\
&\propto \exp\left(
-\frac{\|x_t - \sqrt{\alpha_t}x_{t-1}\|^2}{2(1 - \alpha_t)}
-\frac{\|x_{t-1} - \sqrt{\bar{\alpha}_{t-1}}x_{0}\|^2}{2(1 - \bar{\alpha}_{t-1})}
+\frac{\|x_{t} - \sqrt{\bar{\alpha_{t}}}x_{0}\|^2}{2(1 - \bar{\alpha_{t}})}
\right ) \\
&= \exp\left (
-\frac{1}{2}\left [
\left (\frac{\alpha_t}{\beta_t} + \frac{1}{1-\bar{\alpha}_{t-1}}\right )\|x_{t-1}\|^2
- \left (\frac{2\sqrt{\alpha_t}}{\beta_t}x_t + \frac{2\sqrt{\bar\alpha_{t-1}}}{1 - \bar \alpha_{t-1}} x_0 \right )x_{t-1}
+ C(x_t, x_0)
\right]
\right )
\end{aligned}
q ( x t − 1 ∣ x t , x 0 ) = q ( x t ∣ x 0 ) q ( x t ∣ x t − 1 , x 0 ) q ( x t − 1 ∣ x 0 ) = 2 π ( 1 − α t ˉ ) 1 exp ( − 2 ( 1 − α t ˉ ) ∥ x t − α t ˉ x 0 ∥ 2 ) 2 π ( 1 − α t ) 1 exp ( − 2 ( 1 − α t ) ∥ x t − α t x t − 1 ∥ 2 ) ⋅ 2 π ( 1 − α ˉ t − 1 ) 1 exp ( − 2 ( 1 − α ˉ t − 1 ) ∥ x t − 1 − α ˉ t − 1 x 0 ∥ 2 ) ∝ exp ( − 2 ( 1 − α t ) ∥ x t − α t x t − 1 ∥ 2 − 2 ( 1 − α ˉ t − 1 ) ∥ x t − 1 − α ˉ t − 1 x 0 ∥ 2 + 2 ( 1 − α t ˉ ) ∥ x t − α t ˉ x 0 ∥ 2 ) = exp ( − 2 1 [ ( β t α t + 1 − α ˉ t − 1 1 ) ∥ x t − 1 ∥ 2 − ( β t 2 α t x t + 1 − α ˉ t − 1 2 α ˉ t − 1 x 0 ) x t − 1 + C ( x t , x 0 ) ] )
其中 ∥ x ∥ = x x \|x \| = \sqrt{xx} ∥ x ∥ = x x x t x t − 1 x_t x_{t - 1} x t x t − 1 C ( x t , x 0 ) C(x_t, x_0) C ( x t , x 0 ) x t , x 0 x_t, x_0 x t , x 0 exp ( − ( x − μ ) 2 2 σ 2 ) \exp(-\frac{(x -\mu)^2}{2\sigma^2}) exp ( − 2 σ 2 ( x − μ ) 2 )
可以得到
1 σ 2 = ( α t β t + 1 1 − α ˉ t − 1 ) σ 2 = ( α t β t + 1 1 − α ˉ t − 1 ) − 1 = 1 − α ˉ t − 1 1 − α ˉ t β t μ = 1 2 ( 2 α t β t x t + 2 α ˉ t − 1 1 − α ˉ t − 1 x 0 ) σ 2 = α t ( 1 − α ˉ t − 1 ) 1 − α ˉ t x t + α ˉ t − 1 β t 1 − α ˉ t x 0 \begin{aligned}
\frac{1}{\sigma^2} &= \left (\frac{\alpha_t}{\beta_t} + \frac{1}{1-\bar{\alpha}_{t-1}}\right ) \\
\sigma^2 &= \left (\frac{\alpha_t}{\beta_t} + \frac{1}{1-\bar{\alpha}_{t-1}}\right )^{-1} = \frac{1 - \bar\alpha_{t-1}}{1 - \bar \alpha_t}\beta_t \\
\mu &= \frac{1}{2} \left (\frac{2\sqrt{\alpha_t}}{\beta_t}x_t + \frac{2\sqrt{\bar\alpha_{t-1}}}{1 - \bar \alpha_{t-1}} x_0 \right )\sigma^2 \\
&= \frac{\sqrt{\alpha_t}(1-\bar\alpha_{t-1})}{1-\bar \alpha_t}x_t + \frac{\sqrt{\bar\alpha_{t-1}}\beta_t}{1 - \bar \alpha_t}x_0
\end{aligned}
σ 2 1 σ 2 μ = ( β t α t + 1 − α ˉ t − 1 1 ) = ( β t α t + 1 − α ˉ t − 1 1 ) − 1 = 1 − α ˉ t 1 − α ˉ t − 1 β t = 2 1 ( β t 2 α t x t + 1 − α ˉ t − 1 2 α ˉ t − 1 x 0 ) σ 2 = 1 − α ˉ t α t ( 1 − α ˉ t − 1 ) x t + 1 − α ˉ t α ˉ t − 1 β t x 0
我们希望最后能够不利用 x 0 x_0 x 0 x t = α t ˉ x 0 + 1 − α ˉ t ϵ x_t = \sqrt{\bar{\alpha_t}} x_0 + \sqrt{1 - \bar \alpha_t} \epsilon x t = α t ˉ x 0 + 1 − α ˉ t ϵ x 0 = 1 α ˉ t x t − 1 − α ˉ t α ˉ t ϵ x_0 = \frac{1}{\sqrt{\bar \alpha_t}} x_t - \frac{\sqrt{1 - \bar \alpha_t}}{\sqrt{\bar \alpha_t}}\epsilon x 0 = α ˉ t 1 x t − α ˉ t 1 − α ˉ t ϵ
μ = 1 α t ( x t − β t 1 − α ˉ t ϵ ) \mu = \frac{1}{\sqrt{\alpha_t}}(x_t - \frac{\beta_t}{\sqrt{1 - \bar \alpha_t}}\epsilon)
μ = α t 1 ( x t − 1 − α ˉ t β t ϵ )
所以
x t − 1 ∼ N ( μ , σ 2 ) x_{t - 1} \sim\mathcal N(\mu, \sigma^2)
x t − 1 ∼ N ( μ , σ 2 )
由于高斯噪声 ϵ \epsilon ϵ μ \mu μ x t , t x_t, t x t , t ϵ \epsilon ϵ x t − 1 x_{t - 1} x t − 1
我们希望最终生成出来的概率分布 p θ p_{\theta} p θ q q q H ( p , q ) = E x 0 ∼ q [ − log p θ ( x ] ⩾ E x 0 ∼ q [ − log q ( x 0 ) ] = H ( p ) H(p, q) = \mathbb E_{x_0 \sim q}[-\log p_{\theta}(x_] \geqslant \mathbb E_{x_0\sim q}[-\log q(x_0)] = H(p) H ( p , q ) = E x 0 ∼ q [ − log p θ ( x ] ⩾ E x 0 ∼ q [ − log q ( x 0 ) ] = H ( p )
H ( p , q ) = E x 0 ∼ q [ − log ∫ p θ ( x 0 : T ) d x 1 : T ] \begin{aligned}
H(p, q) &= \mathbb E_{x_0\sim q} \left [-\log \int p_{\theta}(x_{0:T})\text dx_{1:T} \right ]
\end{aligned}
H ( p , q ) = E x 0 ∼ q [ − log ∫ p θ ( x 0 : T ) d x 1 : T ]
这里 ∫ ⋅ d x 1 : T \int \cdot \ \text d x_{1:T} ∫ ⋅ d x 1 : T T T T 1 1 1 p θ ( x 0 : T ) p_{\theta}(x_{0:T}) p θ ( x 0 : T ) x T x_T x T x 1 x_1 x 1
H ( p , q ) = E x 0 ∼ q [ − log ∫ q ( x 1 : T ∣ x 0 ) ⋅ p θ ( x 0 : T ) q ( x 1 : T ∣ x 0 ) d x 1 : T ] = E x 0 ∼ q { − log E x 1 : T ∼ q ∣ x 0 [ p θ ( x 0 : T ) q ( x 1 : T ∣ x 0 ) ] } \begin{aligned}
H(p, q) &= \mathbb E_{x_0\sim q} \left [-\log \int q(x_{1:T}\mid x_0)\cdot \frac{p_{\theta}(x_{0:T})}{q(x_{1:T}\mid x_0)}\text dx_{1:T} \right ] \\
&=\mathbb E_{x_0\sim q} \left \{-\log \mathbb E_{x_{1:T}\sim q\mid x_0} \left [\frac{p_{\theta}(x_{0:T})}{q(x_{1:T}\mid x_0)}\right ] \right \}
\end{aligned}
H ( p , q ) = E x 0 ∼ q [ − log ∫ q ( x 1 : T ∣ x 0 ) ⋅ q ( x 1 : T ∣ x 0 ) p θ ( x 0 : T ) d x 1 : T ] = E x 0 ∼ q { − log E x 1 : T ∼ q ∣ x 0 [ q ( x 1 : T ∣ x 0 ) p θ ( x 0 : T ) ] }
这里 x 1 : T ∼ q ∣ x 0 x_{1:T} \sim q\mid x_0 x 1 : T ∼ q ∣ x 0 x 0 x_0 x 0 x 1 , ⋯ , x T x_{1}, \cdots, x_{T} x 1 , ⋯ , x T
− log ( E ( X ) ) ⩽ E ( − log X ) -\log (\mathbb E(X)) \leqslant \mathbb E(-\log X)
− log ( E ( X ) ) ⩽ E ( − log X )
所以有:
H ( p , q ) ⩽ E x 0 : T ∼ q [ − log p θ ( x 0 : T ) q ( x 1 : T ∣ x 0 ) ] = L V L B \begin{aligned}
H(p, q) &\leqslant \mathbb E_{x_{0:T}\sim q}\left [-\log \frac{p_{\theta}(x_{0:T})}{q(x_{1:T}\mid x_0)}\right ] = L_{VLB}
\end{aligned}
H ( p , q ) ⩽ E x 0 : T ∼ q [ − log q ( x 1 : T ∣ x 0 ) p θ ( x 0 : T ) ] = L V L B
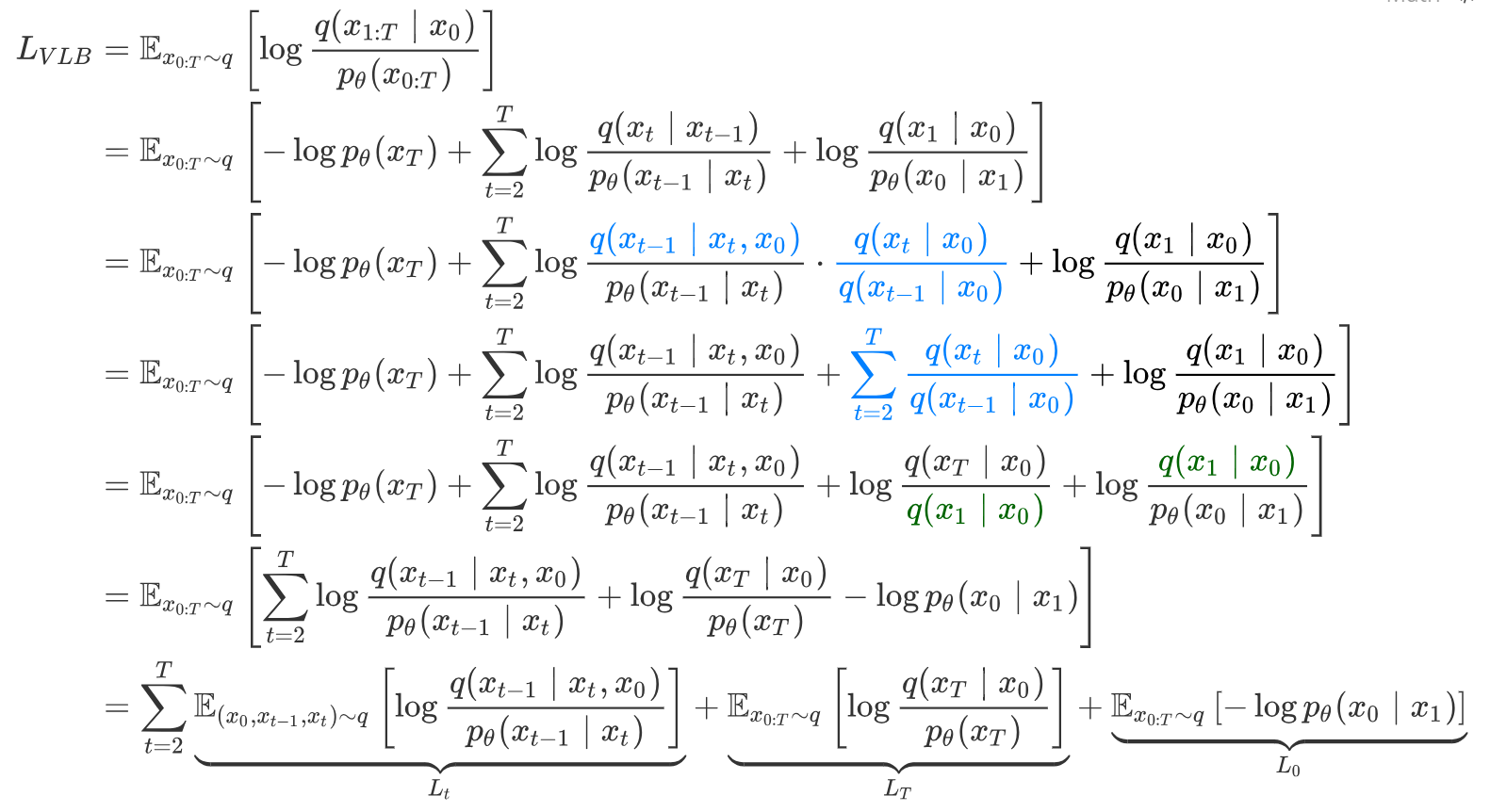
得到的这一项为其变分上界(数学是学不了一点的,这辈子都学不了一点的,明天再说.jpg) ,对其最小化近似于对原函数的最小化。继续化简有:(由于 hexo 博客解析下面这段 latex 有点问题,所以这里用的图片)
其中由于 p θ ( x T ) p_{\theta}(x_T) p θ ( x T ) θ \theta θ L T L_T L T
L t L_t L t 我们对 L t L_t L t
L t = E ( x 0 , x t ) ∼ q [ D K L ( q ( x t − 1 ∣ x t , x 0 ) ∥ p θ ( x t − 1 ∣ x t ) ) ] \begin{aligned}
L_t = \mathbb E_{(x_0, x_t)\sim q}\left [
D_{KL}(q(x_{t-1} \mid x_t, x_0) \| p_{\theta}(x_{t-1}\mid x_t))
\right ]
\end{aligned}
L t = E ( x 0 , x t ) ∼ q [ D K L ( q ( x t − 1 ∣ x t , x 0 ) ∥ p θ ( x t − 1 ∣ x t ) ) ]
由逆向过程的推导我们可以知道 q ( x t − 1 ∣ x t , x 0 ) q(x_{t-1} \mid x_t, x_0) q ( x t − 1 ∣ x t , x 0 ) μ ~ ( x t , x 0 ) \tilde \mu(x_t, x_0) μ ~ ( x t , x 0 ) β ~ t \tilde \beta _t β ~ t p θ ( x t − 1 ∣ x t ) p_{\theta}(x_{t-1}\mid x_t) p θ ( x t − 1 ∣ x t ) μ θ ( x t , t ) \mu_{\theta}(x_t, t) μ θ ( x t , t ) σ t 2 \sigma_t^2 σ t 2
D K L ( N ( μ 1 , σ 1 2 ) ∣ ∣ N ( μ 2 , σ 2 2 ) ) = log σ 2 σ 1 + σ 1 2 + ( μ 1 − μ 2 ) 2 2 σ 2 2 − 1 2 D_{K L}\left(\mathcal{N}\left(\mu_1, \sigma_1^2\right)|| \mathcal{N}\left(\mu_2, \sigma_2^2\right)\right)=\log \frac{\sigma_2}{\sigma_1}+\frac{\sigma_1^2+\left(\mu_1-\mu_2\right)^2}{2 \sigma_2^2}-\frac{1}{2}
D K L ( N ( μ 1 , σ 1 2 ) ∣ ∣ N ( μ 2 , σ 2 2 ) ) = log σ 1 σ 2 + 2 σ 2 2 σ 1 2 + ( μ 1 − μ 2 ) 2 − 2 1
所以有
L t = E ( x 0 , x t ) ∼ q [ 1 2 σ t 2 ∥ μ θ ( x t , t ) − μ ~ ( x t , x 0 ) ∥ 2 + C ] \begin{aligned}
L_t = \mathbb E_{(x_0, x_t)\sim q}\left [
\frac{1}{2\sigma_t^2} \|\mu_{\theta}(x_t, t) - \tilde\mu (x_t, x_0) \|^2 + C
\right ]
\end{aligned}
L t = E ( x 0 , x t ) ∼ q [ 2 σ t 2 1 ∥ μ θ ( x t , t ) − μ ~ ( x t , x 0 ) ∥ 2 + C ]
其中 C C C t t t
μ θ ( x t , t ) = 1 α t ( x t − β t 1 − α ˉ t ϵ θ ( x t , t ) ) μ ~ ( x t , x 0 ) = 1 α t ( x t − β t 1 − α ˉ t ϵ t ) \begin{aligned}
\mu_{\theta}(x_t, t) &= \frac{1}{\sqrt{\alpha_t}}(x_t - \frac{\beta_t}{\sqrt{1 - \bar \alpha_t}}\epsilon_{\theta}(x_t, t)) \\
\tilde \mu(x_t, x_0) &= \frac{1}{\sqrt{\alpha_t}}(x_t - \frac{\beta_t}{\sqrt{1 - \bar \alpha_t}}\epsilon_{t})
\end{aligned}
μ θ ( x t , t ) μ ~ ( x t , x 0 ) = α t 1 ( x t − 1 − α ˉ t β t ϵ θ ( x t , t ) ) = α t 1 ( x t − 1 − α ˉ t β t ϵ t )
化简得
L t = E ( x 0 , x t ) ∼ q [ β t 2 2 σ t 2 α t ( 1 − α ˉ t ) ∥ ϵ θ ( x t , t ) − ϵ t ∥ 2 + C ] L_t = \mathbb E_{(x_0, x_t)\sim q}\left [
\frac{\beta_t^2}{2\sigma_t^2\alpha_t(1-\bar\alpha_t)} \|\epsilon_\theta(x_t, t) - \epsilon_t\|^2 + C
\right ]
L t = E ( x 0 , x t ) ∼ q [ 2 σ t 2 α t ( 1 − α ˉ t ) β t 2 ∥ ϵ θ ( x t , t ) − ϵ t ∥ 2 + C ]
L 0 L_0 L 0 由于原图像每一维的范围是 [ 0 , 255 ] [0, 255] [ 0 , 2 5 5 ] [ − 1 , 1 ] [-1, 1] [ − 1 , 1 ] [ 0 , 255 ] [0, 255] [ 0 , 2 5 5 ] [ x 0 i − 1 255 , x 0 i + 1 255 ] [x_0^{i}-\frac{1}{255}, x_{0}^i + \frac{1}{255}] [ x 0 i − 2 5 5 1 , x 0 i + 2 5 5 1 ] p θ ( x 0 i ∣ x 1 ) p_{\theta}(x_0^i\mid x_1) p θ ( x 0 i ∣ x 1 ) x 0 i x_0^i x 0 i x 0 x_0 x 0 i i i x 0 i = − 1 x_0^i = -1 x 0 i = − 1 x 0 i = 1 x_0^i = 1 x 0 i = 1
p θ ( x 0 ∣ x 1 ) = ∏ i = 1 D ∫ δ − ( x 0 i ) δ + ( x 0 i ) N ( x ; μ θ i ( x 1 , 1 ) , σ 1 2 ) d x δ + ( x ) = { ∞ if x = 1 x + 1 255 if x < 1 δ − ( x ) = { − ∞ if x = − 1 x − 1 255 if x > − 1 \begin{aligned}
p_\theta\left(x_0 \mid x_1\right) & =\prod_{i=1}^D \int_{\delta_{-}\left(x_0^i\right)}^{\delta_{+}\left(x_0^i\right)} \mathcal{N}\left(x ; \mu_\theta^i\left(x_1, 1\right), \sigma_1^2\right) \text d x \\
\delta_{+}(x) & =\left\{\begin{array}{ll}
\infty & \text { if } x=1 \\
x+\frac{1}{255} & \text { if } x<1
\end{array} \quad \delta_{-}(x)= \begin{cases}-\infty & \text { if } x=-1 \\
x-\frac{1}{255} & \text { if } x>-1\end{cases} \right.
\end{aligned}
p θ ( x 0 ∣ x 1 ) δ + ( x ) = i = 1 ∏ D ∫ δ − ( x 0 i ) δ + ( x 0 i ) N ( x ; μ θ i ( x 1 , 1 ) , σ 1 2 ) d x = { ∞ x + 2 5 5 1 if x = 1 if x < 1 δ − ( x ) = { − ∞ x − 2 5 5 1 if x = − 1 if x > − 1
其中 D D D
尽管通过上面两部分,已经可以进行训练, 但是为了实现更方便,使用均方差损失来替代原先的两种损失:
L s i m p l e = E ( x 0 , x t ) ∼ q [ ∥ ϵ ( x t , t ) − ϵ t ∥ 2 ] \begin{aligned}
L_{simple} = \mathbb E_{(x_0, x_t)\sim q} \left [ \|\epsilon(x_t, t) - \epsilon_t\|^2 \right ]
\end{aligned}
L s i m p l e = E ( x 0 , x t ) ∼ q [ ∥ ϵ ( x t , t ) − ϵ t ∥ 2 ]
对于 L t L_t L t
对于 L 0 L_0 L 0 ϵ 0 i − ϵ θ i ( x 1 , 1 ) \epsilon_0^i - \epsilon _\theta^i(x_1,1) ϵ 0 i − ϵ θ i ( x 1 , 1 ) − log p θ ( x 0 ∣ x 1 ) -\log p_{\theta} (x_0 \mid x_1) − log p θ ( x 0 ∣ x 1 ) ∥ ϵ 0 i − ϵ θ i ( x 1 , 1 ) ∥ 2 \|\epsilon_0^i - \epsilon _\theta^i(x_1,1)\|^2 ∥ ϵ 0 i − ϵ θ i ( x 1 , 1 ) ∥ 2
训练的时候,我们从 q ( x 0 ) q(x_0) q ( x 0 ) x 0 x_0 x 0 1 , ⋯ , T 1, \cdots, T 1 , ⋯ , T T T T ϵ ∼ N ( 0 , I ) \epsilon \sim \mathcal N (0, \mathbf I) ϵ ∼ N ( 0 , I ) x t x_t x t ϵ θ ( x t , t ) \epsilon_{\theta}(x_t, t) ϵ θ ( x t , t )
首先我们从 N ( 0 , I ) \mathcal N(\mathbf 0, \mathbf I) N ( 0 , I ) x T x_T x T t = T , T − 1 , ⋯ , 1 t = T, T-1, \cdots, 1 t = T , T − 1 , ⋯ , 1
通过 UNet 预测 t t t ϵ \epsilon ϵ
接着在 N ( 0 , I ) \mathcal N(\mathbf 0, \mathbf I) N ( 0 , I ) z z z t = 1 t = 1 t = 1 z = 0 z = 0 z = 0 x t − 1 x_{t - 1} x t − 1
然后取 x t − 1 = 1 α t ( x t − β t 1 − α ˉ t ϵ ) + 1 − α ˉ t − 1 1 − α ˉ t β t z x_{t - 1} = \frac{1}{\sqrt{\alpha_t}}(x_t - \frac{\beta_t}{\sqrt{1 - \bar \alpha_t}}\epsilon) + \frac{1 - \bar\alpha_{t-1}}{1 - \bar \alpha_t}\beta_t z x t − 1 = α t 1 ( x t − 1 − α ˉ t β t ϵ ) + 1 − α ˉ t 1 − α ˉ t − 1 β t z
参考了一下源代码 的实现,可以看一下这个有注解的版本 ,使用类似 Transformers 的位置编码来对时间步进行编码,然后使用一种复杂度更低的线性注意力 来为 UNet 添加注意力机制。由于没有太理解代码作者把时间编码通过线性层变换后然后均分为两半得到 s , t s, t s , t ( 1 + s ) x + t (1 + s)x + t ( 1 + s ) x + t x x x
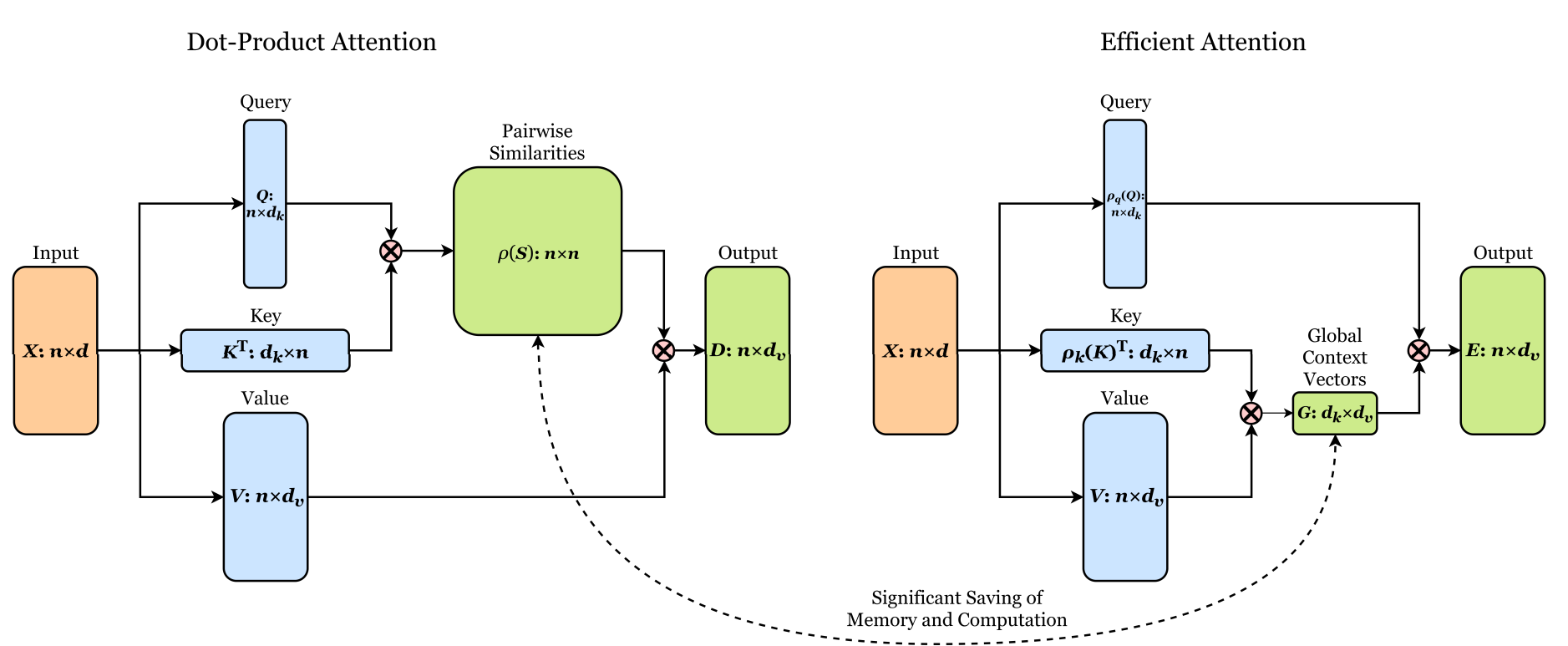
线性注意力优化复杂度的想法是,传统的缩放点积注意力可以看作是计算 ρ ( Q K T ) V \rho(QK^T)V ρ ( Q K T ) V ρ \rho ρ Q K T QK^T Q K T n × n n\times n n × n ρ \rho ρ Q ( K T V ) Q(K^TV) Q ( K T V ) O ( d k d v n ) O(d_kd_vn) O ( d k d v n ) d k d_k d k d v d_v d v n n n ( Q K T ) V (QK^T)V ( Q K T ) V ρ ( Q K T ) ≈ ρ q ( Q ) ρ k ( K T ) \rho(QK^T)\approx \rho_q(Q)\rho_k(K^T) ρ ( Q K T ) ≈ ρ q ( Q ) ρ k ( K T ) ρ \rho ρ ρ q \rho_q ρ q ρ k \rho_k ρ k ρ q ( Q ) ρ k ( K T ) \rho_q(Q)\rho_k(K^T) ρ q ( Q ) ρ k ( K T )
保持每行和为 1 的性质证明如下:
设 A = ρ q ( Q ) ρ k ( K T ) , Q ~ = ρ q ( Q ) , K ~ = ρ k ( K T ) A = \rho_q(Q)\rho_k(K^T), \tilde Q = \rho_q(Q), \tilde K = \rho_k(K^T) A = ρ q ( Q ) ρ k ( K T ) , Q ~ = ρ q ( Q ) , K ~ = ρ k ( K T )
∑ j A i , j = ∑ j ∑ k Q ~ i , k K ~ k , j = ∑ k Q ~ i , k ∑ j K ~ k , j = ∑ K Q ~ i , k = 1 \begin{aligned}
\sum_j A_{i,j} &= \sum_j \sum_k \tilde Q_{i,k} \tilde K_{k, j} \\
&= \sum_k \tilde Q_{i, k} \sum_j \tilde K_{k, j} \\
&= \sum_K \tilde Q_{i, k} \\
&= 1
\end{aligned}
j ∑ A i , j = j ∑ k ∑ Q ~ i , k K ~ k , j = k ∑ Q ~ i , k j ∑ K ~ k , j = K ∑ Q ~ i , k = 1
网络中的注意力层实现如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 class CrossAttention (nn.Module) : def __init__ (self, num_input, num_heads=4 , dim_heads=32 , *, bias=False ) : super ().__init__() self.scale = math.pow (dim_heads, -0.5 ) self.num_heads = num_heads num_hiddens = num_heads * dim_heads self.C_qkv = nn.Conv2d(num_input, num_hiddens * 3 , 1 , bias=bias) self.W_vh = nn.Linear(num_input, num_hiddens, bias=bias) self.C_hy = nn.Conv2d(num_hiddens, num_input, 1 ) def forward (self, X, Vt ) : ''' - X: Images, with a shape of (batch_size, num_channels=num_input, x, y) - V1: Time encoding, with a shape of (batch_size, num_hiddens=num_input) ''' x = X.shape[-2 ] QKV = self.C_qkv(X).chunk(3 , dim=1 ) Vt = self.W_vh(Vt) Q, K, V = tuple (rearrange(t, 'b (h d) x y -> b h d (x y)' , h=self.num_heads) for t in QKV) Vt = rearrange(Vt, 'b (h d) -> b h d 1' , h=self.num_heads) K = torch.concat([K, Vt], dim=-1 ) V = torch.concat([V, Vt], dim=-1 ) Q = Q * self.scale sim = torch.einsum('b h d i, b h d j -> b h i j' , Q, K) sim = sim - sim.amax(dim=-1 , keepdim=True ).detach() attn = sim.softmax(dim=-1 ) Y = torch.einsum('b h q k, b h d k -> b h q d' , attn, V) Y = rearrange(Y, 'b h (x y) d -> b (h d) x y' , x=x) return self.C_hy(Y) class CrossLinearAttention (nn.Module) : def __init__ (self, num_input, num_heads=4 , dim_heads=32 , *, bias=False ) : super ().__init__() self.scale = math.pow (dim_heads, -0.5 ) self.num_heads = num_heads num_hiddens = num_heads * dim_heads self.C_qkv = nn.Conv2d(num_input, num_hiddens * 3 , 1 , bias=bias) self.W_vh = nn.Linear(num_input, num_hiddens, bias=bias) self.C_hy = nn.Conv2d(num_hiddens, num_input, 1 ) def forward (self, X, Vt ) : x = X.shape[-2 ] QKV = self.C_qkv(X).chunk(3 , dim=1 ) Vt = self.W_vh(Vt) Q, K, V = tuple (rearrange(t, 'b (h d) x y -> b h d (x y)' , h=self.num_heads) for t in QKV) Vt = rearrange(Vt, 'b (h d) -> b h d 1' , h=self.num_heads) K = torch.concat([K, Vt], dim=-1 ) V = torch.concat([V, Vt], dim=-1 ) Q = Q.softmax(dim=-2 ) K = K.softmax(dim=-1 ) context = torch.einsum('b h d n, b h e n -> b h d e' , K, V) Y = torch.einsum('b h d e, b h d n -> b h e n' , context, Q) Y = rearrange(Y, 'b h c (x y) -> b (h c) x y' , x=x) return self.C_hy(Y)
接着参考了原作者的实现,对 UNet 的架构进行了一些简单的修改:
将卷积层替换为 2 个 3x3 卷积层组成的残差块
在上采样和下采样之前添加注意力层,注意力层除了包含图像每个点的键值和查询外,额外添加一对时间编码的键值
在 UNet 的最下层采用缩放点积注意力,其余部分使用线性注意力
上采样层和下采样层,以及 UNet 的实现如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 class CADown (nn.Module) : def __init__ (self, in_channels, out_channels, time_dim, *, num_groups=8 , bias=False ) : super ().__init__() self.res1 = ResnetBlock(in_channels, out_channels, num_groups) self.res2 = ResnetBlock(out_channels, out_channels, num_groups) self.mlp1 = nn.Sequential( nn.SiLU(), nn.Linear(time_dim, out_channels) ) self.norm = nn.GroupNorm(1 , out_channels) self.attn = Residual(CrossLinearAttention(out_channels, bias=bias)) self.down = nn.MaxPool2d(kernel_size=2 , stride=2 ) def forward (self, X, T, stk ) : X = self.res1(X) stk.append(X) X = self.res2(X) stk.append(X) T = self.mlp1(T) X = self.norm(X) X = self.attn(X, T) return self.down(X) class CAUp (nn.Module) : def __init__ (self, in_channels, out_channels, time_dim, *, num_groups=8 , bias=False ) : super ().__init__() self.up = nn.ConvTranspose2d(in_channels, out_channels, 2 , 2 ) self.res1 = ResnetBlock(in_channels, out_channels, num_groups) self.res2 = ResnetBlock(in_channels, out_channels, num_groups) self.mlp1 = nn.Sequential( nn.SiLU(), nn.Linear(time_dim, out_channels) ) self.norm = nn.GroupNorm(1 , out_channels) self.attn = Residual(CrossLinearAttention(out_channels, bias=bias)) def forward (self, X, T, stk ) : X = self.up(X) X = torch.concat((X, stk.pop()), dim=1 ) X = self.res1(X) X = torch.concat((X, stk.pop()), dim=1 ) X = self.res2(X) T = self.mlp1(T) X = self.norm(X) return self.attn(X, T) class ConditionalUNet (nn.Module) : def __init__ (self, in_channels, init_channels, out_channels, time_emb_dim, num_layers=4 , *, num_groups=8 , attn_bias=False ) : super ().__init__() down_block = partial(CADown, num_groups=num_groups, bias=attn_bias) up_block = partial(CAUp, num_groups=num_groups, bias=attn_bias) dim = in_channels self.emb_t = SinusoidalPositionEmbedding(time_emb_dim) self.mlp_t = nn.Sequential( nn.Linear(time_emb_dim, time_emb_dim), nn.GELU(), nn.Linear(time_emb_dim, time_emb_dim) ) self.downs = nn.ModuleList([]) for i in range (num_layers) : out_dim = dim * 2 if i > 0 else init_channels self.downs.append(down_block(dim, out_dim, time_emb_dim)) dim = out_dim self.mid_res1 = ResnetBlock(dim, dim * 2 , num_groups) dim *= 2 self.mid_norm = nn.GroupNorm(1 , dim) self.mid_mlp = nn.Sequential( nn.SiLU(), nn.Linear(time_emb_dim, dim) ) self.mid_attn = Residual(CrossAttention(dim)) self.mid_res2 = ResnetBlock(dim, dim, num_groups) self.ups = nn.ModuleList([]) for i in range (num_layers) : self.ups.append(up_block(dim, dim // 2 , time_emb_dim)) dim = dim // 2 self.final_conv = nn.Conv2d(dim, out_channels, 1 ) def forward (self, X, time ) : T = self.emb_t(time) T = self.mlp_t(T) stk = [] for blk in self.downs : X = blk(X, T, stk) X = self.mid_res1(X) X = self.mid_attn(self.mid_norm(X), self.mid_mlp(T)) X = self.mid_res2(X) for blk in self.ups : X = blk(X, T, stk) return self.final_conv(X)
使用 CelebA 数据集,UNet 使用 4 层(进行 4 次下采样),初始通道数 64,扩散的过程取 T = 1000 T=1000 T = 1 0 0 0 β \beta β 1 0 4 10^4 1 0 4 0.02 0.02 0 . 0 2
分别对 t = 200 , 500 , 900 t = 200, 500, 900 t = 2 0 0 , 5 0 0 , 9 0 0
采样结果如下
虽然效果不佳,但是已经初具人形了
时间步较小时去噪的均方差损失会较大,当时以为需要去平衡一下这里的损失,于是训练时根据每个时间步上次的损失再归一化的方式对时间步进行采样,反而导致从时间步较大进行还原时的效果非常差,以至于最终生成的结果所有地方几乎一个颜色:
后来改成训练时对每个时间步均匀采样即可得到前面提到的初具人形的结果。



 。
。
