强化学习笔记

强化学习（reinforcement learning，RL）讨论的问题是智能体怎么在复杂、不确定的环境里面去最大化它能获得的奖励。强化学习中主要有两部分：智能体和环境。

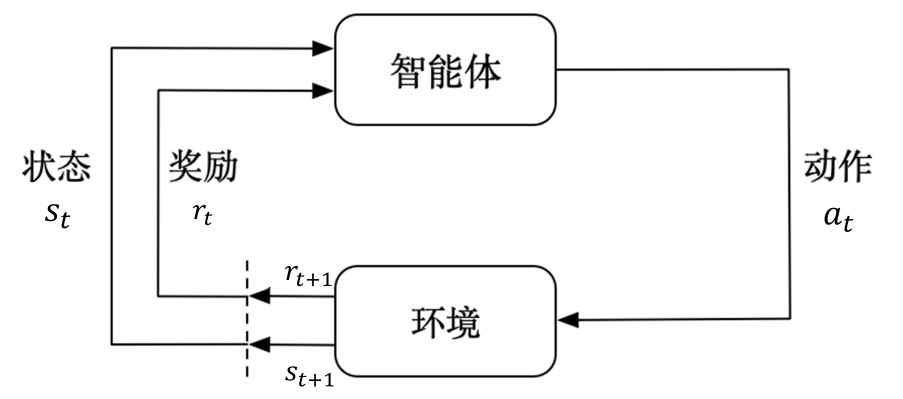
在强化学习中，与一般的机器学习问题，例如分类、回归等，有一些明显的区别：

• 强化学习中存在延迟奖励的问题。比如智能体采取了一步行动，没有办法立刻知道这一步是好的决策还是坏的决策，可能要到很多步之后，才能取得最终的结果。
• 智能体得到的观测是和时间相关的，前一时刻和当前时刻有很大的关系，但是机器学习中不同样本一般是独立的。

这里的观测与状态有一些区别：比如说走迷宫，状态应该是智能体在迷宫的什么位置，但是智能体至多知道自己经过的路是什么样的，而没法直接确定整个迷宫。具体地来说，状态是对环境的完整的描述，而观测可能只是对环境的部分描述，即智能体能观测到的信息。

Markov 决策过程

Markov 过程做出如下假设：下一步的状态仅与当前状态有关。

Markov 奖励过程

普通的 Markov 过程中只包含到达每个状态的概率，而 Markov 奖励过程则是在 Markov 过程中加入奖励。

由于游戏可能由很多步，每一步都会有奖励，我们通常希望越早得到越多的奖励，因此我们引入回报的概念。这里回报根据一个折扣因子 $\gamma$ ，用指数衰减的形式进行建模：设对于某个决策过程， $t$ 时刻以及之后能获得的回报为 $G_t$，那么有：

$$G_t = r_{t} + \gamma r_{t+1} + \cdots + \gamma^{T - t} r_{T}$$

其中 $r_t$ 表示在 $t$ 时刻获得的奖励，其中 $T$ 表示最终的时刻。

为了比较两个状态哪个更好，这里继续定义状态价值函数，我们用 $V(s, t)$ 表示 $t$ 时刻在状态 $s$，之后所能获得的期望回报。这里并没有决策过程，只是按照状态 $u$ 到 $v$ 的概率进行随机游走，因此这里只能定义为期望，而不是最大值。很容易能写出 $V(s, t)$ 的转移式子：

$$V(s, t) = R(s) + \gamma \sum_{s'} P(s'\mid s)V(s')$$

即所谓的 Bellman 方程。

Markov 决策过程

Markov 决策过程则是在 Markov 奖励过程再加上决策过程。对于每个状态 $s$，智能体先做出决策 $a$，然后根据决策 $s$ 和决策 $a$ 得到到达新的状态 $s'$ 的概率。我们为这个决策过程也赋予一个函数，称为决策函数 $\pi$，$\pi(a\mid s)$ 用于衡量在状态为 $s$ 时，我们做出决策 $a$ 的概率。

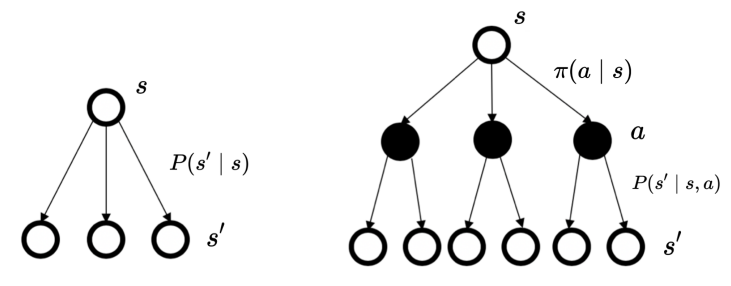
这里假定 $\pi$ 为一个已知的函数，那么状态之间转移的概率也便是一个定值了，我们用 $P_\pi(s' \mid s)$ 来表示在策略 $\pi$ 下，从 $s$ 转移到 $s'$ 的概率。

奖励函数与状态和决策都有关系，我们定义 $r_{\pi}(s)$ 来使得外层的过程避开对决策的考虑。我们根据 $P_{\pi}$ 和 $r_{\pi}$ 即可用同样的方法定义出价值函数 $V_\pi$。为了计算 $V_{\pi}$，我们引入另一个函数 $Q$，即动作价值函数，用于描述在某一状态采取某一个决策，得到的回报的期望，即

$$Q_\pi(s, a) = \mathbb E_\pi[G_t\mid s_t = s, a_t = a]$$

那么有

$$V_\pi(s) = \sum_{a} \pi(a\mid s)Q_\pi(s, a) \\ Q_\pi(s,a) = R(s,a) + \gamma\sum_{s'} P(s' \mid s, a)V_{\pi}(s')$$

现在当 $\pi$ 给定的时候，我们可以将其抽象为一个与 Markov 奖励过程类似的过程。

Markov 决策过程控制

在 Markov 决策过程中，有两个最核心的问题：

• 预测问题（prediction）：求解每个状态的价值
• 控制问题（control）：寻找最佳策略 $\pi^*$ 及其对应的最佳价值 $V_{\pi^*}$

解决控制问题一般有两种迭代的方法：策略迭代和价值迭代。

策略迭代

策略迭代由两部分组成：

• 策略评估：根据当前的 $\pi$ 计算每个状态的价值 $V$
  价值函数一般通过枚举步数，然后迭代更新。
• 策略提升：根据 $V$ 来对策略进行调整
  一种方法是根据 $V$ 来计算 $Q$ 函数，然后我们对于修改 $\pi$ 使得对于每个状态能取到它最优的 $Q$。

价值迭代

价值迭代的想法是先计算出最优的 $V$，然后再想办法通过 $V$ 来求出相应的策略。这里假定对于每个状态 $s$ 仅会有 1 种决策，而不是再多种决策中随机。

由于在最优方案中需要满足

$$V(s) = \max_a Q(s,a)$$

如果 $V$ 不是最优方案，那么我们可以重新用上面等式计算出 $V'$，然后将 $V$ 更新为 $V'$，由此迭代进行，直到 $V$ 收敛或达到指定上限迭代次数。

迭代结束后得到的 $V^*$，我们可以根据 $V^*$ 计算出 $Q^*$ 然后对于每个状态使得 $Q^*$ 取得最大值的动作 $a$ 作为在它的决策。

表格型方法

免模型预测

• 蒙特卡洛方法：寻找大量决策的过程，根据每个状态到达的次数和每次之后获得的奖励来估计它的价值函数。

• 时序差分：综合了蒙特卡洛方法和动态规划，假设根据策略 $\pi$，某一次游戏过程到达的状态依次为 $s_1, s_2, \cdots$，那么对于每一步，可以根据此时的 $V$，也就是对价值函数的估计，来更新：

  $$V(s_t) \leftarrow V(s_t) + \alpha[(r_{t} + \gamma V(s_{t + 1})) - V (s_t)]$$

  其中 $\alpha$ 为学习率。
  可以理解是利用每次重新估计的价值和以前估计的的差来更新价值函数。

• $n$ 步时序差分：再走 $n$ 步后，再利用上述公式更新。

免模型控制

Sarsa 算法

Sarsa 算法和时序差分的想法类似，不过 Sarsa 算法直接去维护 Q 函数

$$Q(s_t, a_t) \leftarrow Q(s_t, a_t) + \alpha [R(s_t,a_t) + \gamma Q(s_{t + 1}, a_{t + 1}) - Q(s_t, a_t)]$$

在执行策略的时候一般采用 $\epsilon$ 贪心，以 $1 - \epsilon$ 的概率根据 $Q$ 选择最优解，以 $\epsilon$ 的概率做出随机决策。一般随着训练的进行，$\epsilon$ 逐渐减小。

Sarsa 算法会直接对当前正在进行的策略进行更新，因此 Sarsa 算法是一种同策略（on-policy）算法

Q-learning 算法

Q-learning 是一种异策略（off-policy）算法。异策略在学习的过程中会涉及到两种不同的策略：

• 目标策略：我们希望去学习的策略，一般不需要和环境直接去交互
• 行为策略：行为策略是指探索环境的策略，一般用 $\mu$ 来表示，它会去大胆地探索环境，然后将获取到的数据提供给目标策略学习。

Q-learning 也是采用时序差分的想法来维护 $Q$ 函数，具体两种策略如下：

• 行为策略：根据当前的 $Q$ 按照随机策略或者 $\epsilon$ 贪心选取动作 $a$，然后获取动作 $a$ 执行后状态 $s'$
• 目标策略：根据 $Q$ 以及 $s$ 选取最优的 $a$。

虽然看上去它和 Sarsa 算法很像，但是有一些不同：

• Sarsa 算法中间下一步动作（$a_{t+1}$）是通过当前的策略（$\epsilon$ 贪心策略）得到的

• 而 Q-learning 在更新 $Q$ 的时候，会认为在 $s'$ 之后会根据目标策略进行操作，因此 Q-learning 的更新式为：

  $$Q(s, a) \leftarrow Q(s, a) + \alpha[R(s, a) + \gamma \max_{a'} Q(s', a') - Q(s, a)]$$

  其中 $\max$ 项就是目标策略决策的部分。

深度强化学习

策略梯度

我们这里策略 $\pi$ 也用一个神经网络来表示，输入是状态，输出是每种动作执行的概率。

设 $\tau$ 为某一次游戏过程，$R(\tau)$ 为这次游戏过程获得的奖励，$P_\pi (\tau)$ 表示根据策略 $\pi$ 进行游戏，游戏过程为 $\tau$ 的概率。那么根据策略 $\pi$ 获得奖励的期望可以表示为：

$$\mathbb E[R] = \sum_{\tau} R(\tau) P_{\pi}(\tau)$$

我们希望去做一个梯度上升去优化 $\pi$，因此我们会希望去求它关于 $\pi$ 的参数的梯度，于是有：

$$\begin{aligned} \nabla \mathbb E(R) &= \sum_\tau R[\tau] \nabla P_{\pi}(\tau) \\ &= \sum_{\tau} R(\tau) P_{\pi} (\tau) \frac{\nabla P_{\pi}(\tau)}{P_{\pi}(\tau)} \\ &= \sum_{\tau} R(\tau) P_{\pi} (\tau) \nabla\log P_{\pi}(\tau) \\ &=\mathbb E[R(\tau )\cdot \nabla \log P_{\pi}(\tau)] \end{aligned}$$

计算 $\nabla \log P_{\pi}(\tau)$ 相当于我们只用对其中每一个决策的概率 $\log P(a_i \mid s_i)$ 用反向传播求出梯度，再求和就可以了。

但实际上我们不太可能去直接计算 $\nabla \mathbb E(R)$，我们一般选取 $N$ 次游戏过程，用它们的 $R (\tau)\cdot \nabla \log P_{\pi} (\tau)$ 的均值作为 $\nabla \mathbb E(R)$ 的近似值。

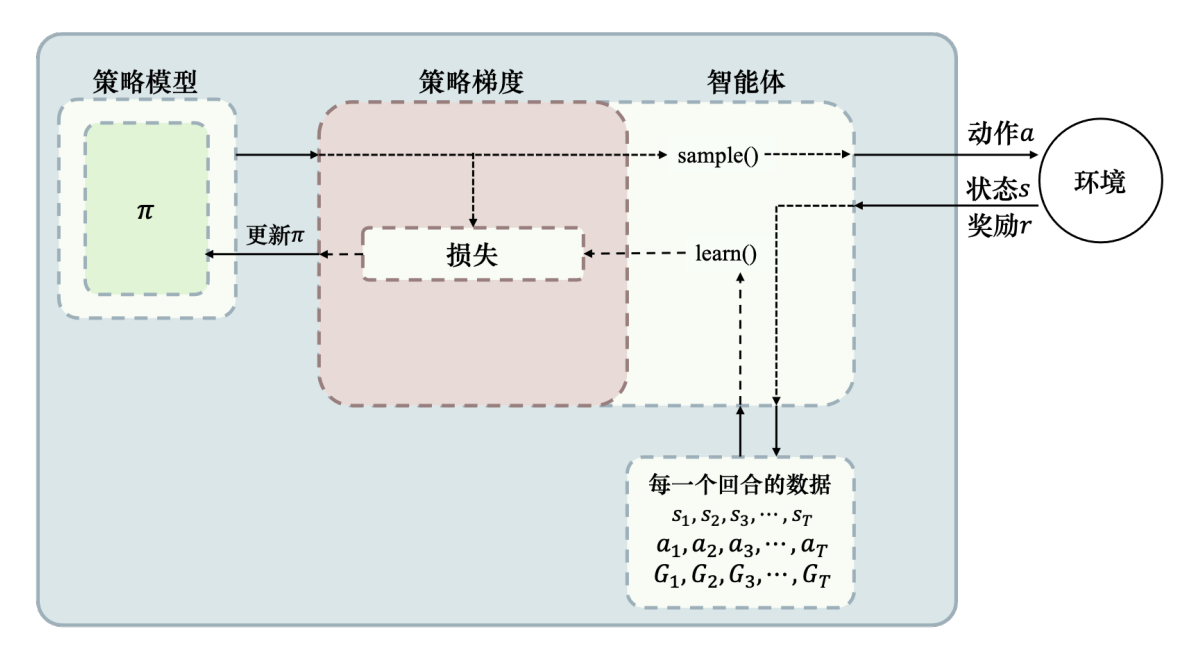
添加基线

假如一个游戏的奖励总是正的，现在有 3 个动作 $a, b, c$，可能进行动作 $a$ 效果最好，但是由于各种原因很难采样到 $a$，总是采样到 $b$，由于奖励总是正的，这会导致我们算法总是会去提高动作 $b$ 的概率。这不是我们想要的结果，因此我们在计算一次游戏的奖励的时候，我们把奖励减去某个 $b$，这个 $b$ 称为基线（baseline）。一般这个 $b$ 会取为 $\mathbb E [R(\tau)]$。但一般不会单独去求，而是在训练的过程中，不断记录 $R(\tau)$，根据历史和当前的计算一个加权平均值，让这个作为 $\mathbb E[R(\tau)]$ 的估计值。

为 状态-动作 分配分数

这里想解决的问题是这样的：我们在做梯度上升的时候，相当于根据 $R$ 的大小来往这个方向上调整 $\pi$。假如一次游戏中 $R$ 是正的，那么梯度上升相当于会希望中间每一个 状态-动作 的出现概率会增大。这里我们为同一个游戏中，不同的动作分配了相同分数，但实际上有些动作可能是好的，有些动作可能是不好的。当采样足够多的时候，这可能不是一个大问题。但是当采样不充足的时候，这样统计出来的分数是不合理的。因此我们的想法是为每个状态-动作重新设计它的分数。

这里我们直接修改计算的梯度，我们将对于一个状态动作对的系数改变为进行完它，在之后的时间内所获得的奖励。我们也希望执行完这个动作能尽可能快地获得奖励，因此类似前面的做法，我们将累积的奖励再乘上一个衰减因子：

$$\frac{1}{N}\sum_{n=1}^N \sum_t \left (\sum_{t' \geqslant t} \gamma ^{t' - t}r^{(n)}_{t'} - b\right ) \nabla \log P_{\pi} (a^{(n)}_t\mid s_{t}^{(n)})$$

其中 $b$ 是基线，实现的时候会让 $b$ 和状态相关，我们也用一个网络来估计它。我们称 $R - b$ 这一项为优势函数，用 $A^{\pi}(s, a)$ 来表示在策略 $\pi$ 下，在状态 $s$ 中采取动作 $a$，相较于基线有多少优势。

近端优化策略（PPO）

重要性采样

在策略梯度算法中，每更新一次模型会导致之前的数据被丢弃，然后重新采样，这样会非常地耗时间。PPO 的想法是采集一次数据用于多轮更新。

这里带来了第一个问题，我们计算期望是 $\mathbb E_{\tau \sim P_{\pi}}[R \cdot \nabla \log P_{\pi}]$，我们现在只能从另一个分布 $P_{\pi'}$ 中采样。现在我们希望做一个修正。注意到：

$$\begin{aligned} \mathbb E_{\tau \sim P_\pi} [R\cdot \nabla \log P_\pi] &= \sum_{\tau} P_{\pi}(\tau) R(\tau) \nabla \log P_\pi(\tau) \\ &= \sum_{\tau} P_{\pi'}(\tau) \frac{P_{\pi}(\tau)}{P_{\pi'}(\tau)} \nabla \log P_{\pi}(\tau) \\ &= \mathbb E_{\tau \sim P_{\pi'}}\left [\frac{P_{\pi}}{P_{\pi'}} \cdot R\cdot \nabla \log P_{\pi} \right ] \end{aligned}$$

因此我们采样的时候将计算的期望乘上概率的比值即可。这一方法称为重要性采样。

近端策略优化

接下来我们再采用策略梯度中的一些小技巧，为每个状态-动作对单独赋予权重，再用重要性采样避免每次都重新采样，现在的优化目标是：

$$J^{\pi'}(\pi) = \mathbb E_{(s_t, a_t)\sim \pi'}\left [\frac{P_{\pi}(a_t \mid s_t)}{P_{\pi'}(a_t\mid s_t)} A^{\pi'}(s_t, a_t) \right ]$$

如果 $\pi$ 和 $\pi'$ 相差太多，那么容易导致计算的期望不太准确，一部分原因是因为重要性采样在采样不充足的时候方差较大，更进一步的细节可以看蘑菇书上的证明。另一部分原因是优势函数的值也会相差较多。

PPO 要做的事情就是防止 $\pi$ 和 $\pi'$ 相差过多。 下面介绍它的前身算法，和它的两种常见的实现

• （信任区域策略优化，TRPO）TRPO 使用 KL 散度来衡量 $\pi'$ 和 $\pi$ 的差异。其中 $KL$ 散度通过如下方法计算：

  $$KL(\pi, \pi') = \mathbb E_{(s, a) \sim \pi} \left [\log \frac{P_{\pi}(a\mid s) }{P_{\pi'}(a\mid s)}\right ]$$

  这里 KL 散度蘑菇书上没讲怎么算，应该也是通过采样来估计。

  TRPO 的想法是限制 $KL(\pi, \pi') < \epsilon$ ，在这种情况下去优化 $J^{\pi'}(\pi)$。具体实现方法比较复杂，这里略去。

• （近端策略优化惩罚，PPO-penalty）PPO-penalty 的想法很简单，直接把 TRPO 中的约束变为一个惩罚项即可：

  $$J^{\pi'}_{PPO}(\pi) = J^{\pi'}(\pi) - \beta KL(\pi, \pi')$$

  其中 $\beta$ 是一个超参数。$\beta$ 的取值一般通过设置 $KL$ 的范围来动态调整，当超过上界时，增加 $\beta$，小于的话，减少 $\beta$。

• （近端策略优化裁剪，PPO-clip）PPO-clip 的想法就很简单，如果 $\pi$ 和 $\pi'$ 差得比较多，那么我们认为是因为某些 $\frac{P_{\pi}(a\mid s) }{P_{\pi'}(a\mid s)}$ 落在 $[1 - \epsilon, 1 + \epsilon]$ 外面。这个时候我认为它只修改到了它最大能修改到的范围，这样求梯度的时候，这一项会变成 0。但是这里面稍微有一点例外的是：如果我把模型变差了，即在某个 $(a, s)$ 处，$\frac{P_{\pi}}{P_{\pi'}} A$ 的取值反而比原来小了，那么这个时候我们认为这里还要进行优化，而不是不去做更改。这里优化的肯定就会向原来的方向进行优化，即离 $\pi'$ 更近，也是我们想要的结果。PPO-clip 的目标式子可以写为：

  $$J^{\pi'}_{PPO2}(\pi) = \mathbb E_{(s, a) \sim \pi'} \left[ \min\left \{\frac{P_{\pi}(a_t \mid s_t)}{P_{\pi'}(a_t\mid s_t)} A^{\pi'}(s_t, a_t) ， \\ \text{clip}\left (\frac{P_{\pi}(a_t \mid s_t)}{P_{\pi'}(a_t\mid s_t)}, 1-\epsilon, 1+\epsilon\right ) A^{\pi'}(s_t, a_t) \right \}\right]$$

  其中 clip 函数可以见下图：

  

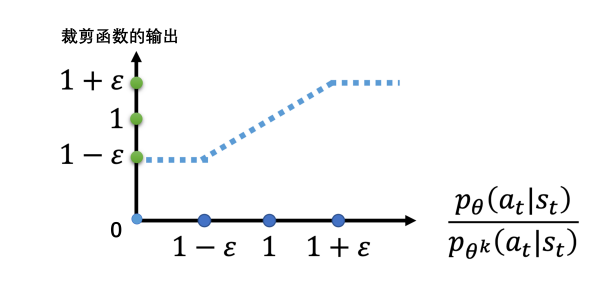
  这个取 min 最终的效果如下图，可以看作就是给向好的方向修正的时候，给偏离 $\pi'$ 的程度一个限制：

  

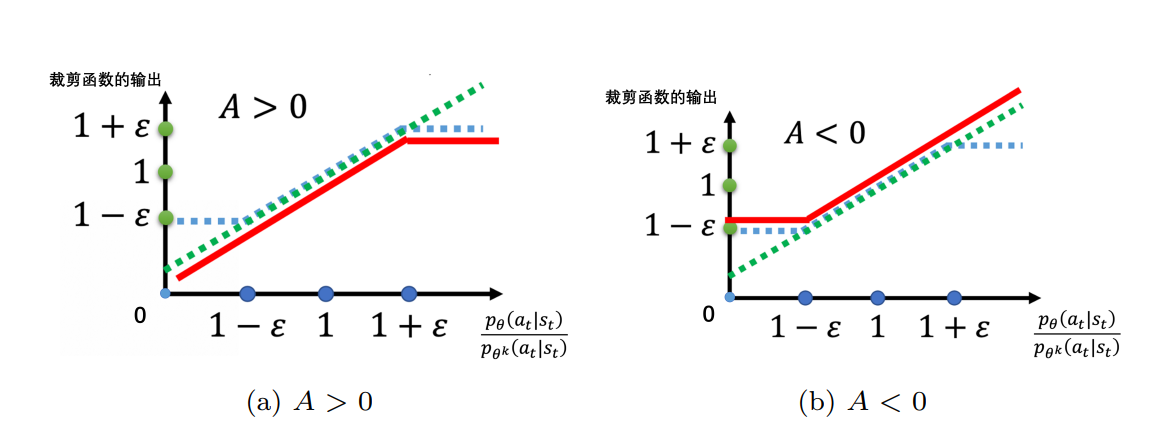
深度 Q 网络（DQN）

传统的强化学习以表格的形式存储 $V$ 和 $Q$，但实际问题中状态数可能相当多，或者状态空间是连续的，这种情况下难以直接用表格进行存储。这时候我们用一个神经网络来近似 $V$ 或者 $Q$。

我们需要把 $V$ 函数换成一个网络带来的问题是我们怎么去训练这个网络。这里也有两种方法：

• 基于蒙特卡洛的想法：我们选取初始状态 $s$，然后根据策略 $\pi$ 去玩这个游戏，那么我可以统计每一步获得的奖励，最终相当于我会得到若干形如 从 $s$ 根据策略 $\pi$ 进行游戏，能获得 $G_s$ 奖励 的数据 ，然后做一个回归问题的学习。
• 基于时序差分的想法：我们仍然也是选取一些初始状态 $s$，然后根据策略 $\pi$ 去玩游戏，但是我们这里只会统计它的下一步能得到多少奖励，比如 $r$，然后根据时序差分的式子，我们相当于希望能满足 $\gamma V(s') + r = V(s)$，那么我们去最小化在我们得到的样本上它们的差值。

对于 $Q$ 网络的学习是类似的方法。

这里存在一个问题，对于新的状态 $s'$ 会随着策略变更而改变，这样会导致训练的过程不太稳定。因此一般的做法是，希望去固定 $\gamma Q(s', \pi(s')) + r$，于是我们取某一时刻的 $Q$ 网络，将它的参数固定住，作为目标网络 $\hat Q$，然后用 $\gamma \hat Q(s', \pi(s')) + r$ 作为 $V(s)$ 的目标值去做回归。然后再在 $Q$ 训练了若干次之后，再用 $Q$ 的参数覆盖 $\hat Q$。

现在有了 $Q$ 函数，我们可以通过下面过程来强化学习：

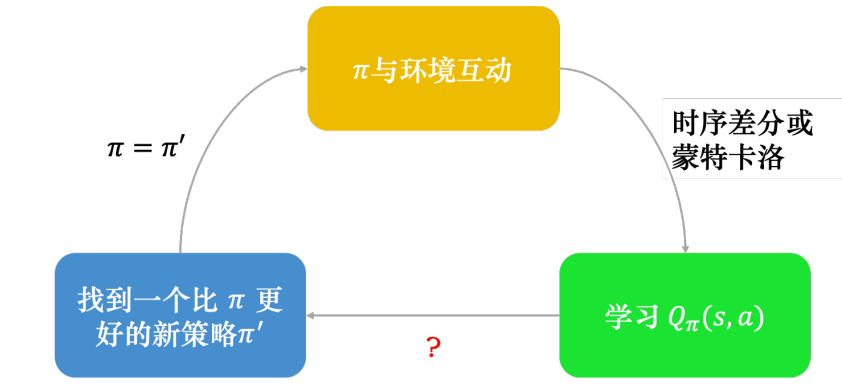
但是这里出现一个问题，我们怎么来根据 $Q$ 网络来得到一个更好的策略？我们还是希望像 Q-learning 那样，对于每个状态 $s$ 根据 $Q$ 选择此时最优的动作 $a$ 。但这里状态数很大，我们会用一个神经网络来表示策略 $\pi$。但感觉蘑菇书没讲这个问题。感觉应该是对通过采样得到的数据，然后考虑其中的状态 $s_t$，然后计算它的最优动作，相当于得到了一些训练数据，然后根据此来更新策略网络。